Content by Harish Jose

Tue, 02/05/2019 - 12:03
The TV show The Walking Dead, about survival in a post-apocalyptic zombie world, is one of the top-rated currently. I’ve written previously about the show, but today I want to briefly look at the complex adaptive systems (CAS) in the show’s plot…
Thu, 01/03/2019 - 12:03
One of my favorite things to do when I learn new and interesting information is to apply it to a different area to see if I can gain further insight. Here, I am looking at the principle, “Chekhov’s gun,” named after the famous Russian author, Anton…
Wed, 10/24/2018 - 12:02
I am writing today about “bootstrap kaizen.” This is something I have been thinking about for a while. Wikipedia describes bootstrapping as “a self-starting process that is supposed to proceed without external input.” The term was developed from a…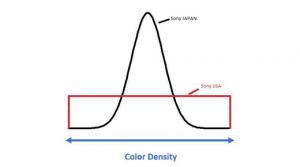
Tue, 10/02/2018 - 12:03
I am a quality manager by profession. Thus, I think about quality a lot. How would one define “quality?” A simple view of quality is “conformance to requirements.” This simplistic view of quality lacks the complexity that it should have. It assumes…
Mon, 08/27/2018 - 12:03
I came across an interesting phrase recently. I was reading Kozo Saito’s paper, “Hitozukuri and Monozukuri,” and I saw the phrase “kufu eyes.” Kufu is a Japanese word that means “to seek a way out of a dilemma.” This is very well explained in…
Mon, 07/02/2018 - 12:03
I have written about sample size calculations many times before. One of the most common questions a statistician is asked is, “How many samples do I need—is a sample size of 30 appropriate?” The appropriate answer to such a question is always, “It…
Wed, 05/09/2018 - 12:01
I have been writing about kaizen a lot recently. It is a simple idea: change for the better. Generally, kaizen stands for small incremental improvements. Here I’m going to look at what is the best kind of kaizen.
The twist in the dumpling
A few…
Mon, 03/12/2018 - 13:02
In today’s column, I will be looking at kaizen and kaikaku through the lens of the explore/exploit model. Kaizen is often translated from Japanese as “continuous improvement” or “change for better.” Kaikaku, another Japanese term, is translated as…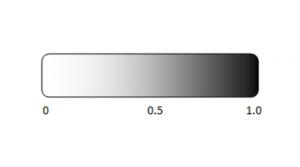
Thu, 02/01/2018 - 12:02
It’s not easy to find topics to write about, and even if I find good topics, it has to pass my threshold level. As I was meditating on this, I started to think about procrastination and ambiguity. So my column today is about the importance of “…
Thu, 12/14/2017 - 12:02
I recently read Jordan Ellenberg’s wonderful book, How Not To Be Wrong: The Power of Mathematical Thinking (Penguin Books, 2014). I found the book to be enlightening and a great read. Ellenberg has the rare combination of being knowledgeable and…