I have written about sample size calculations many times before. One of the most common questions a statistician is asked is, “How many samples do I need—is a sample size of 30 appropriate?” The appropriate answer to such a question is always, “It depends!”

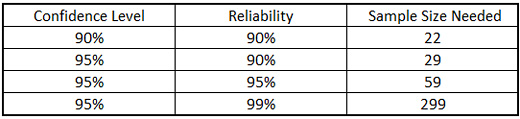
In today’s column, I have attached a spreadsheet that calculates the reliability based on Bayesian Inference. Ideally, one would want to have some confidence that the widgets being produced is X-percent reliable, or in other words, it is X-percent probable that the widget would function as intended. The ubiquitous 90/90 or 95/95 confidence/reliability sample size table is used for this purpose.

 …