Many have been taught that they must remove outliers prior to analysis. This is because much of modern statistics is concerned with creating a mathematical model for the data. Because all these models are created using algorithms, they tend to be severely affected by any unusual or extreme values.
Therefore, to use these mathematical techniques to obtain useful and appropriate models, it’s often necessary to polish up the data by removing the outliers. However, the act of building a model implicitly assumes that the data are homogeneous enough to justify the use of a model.
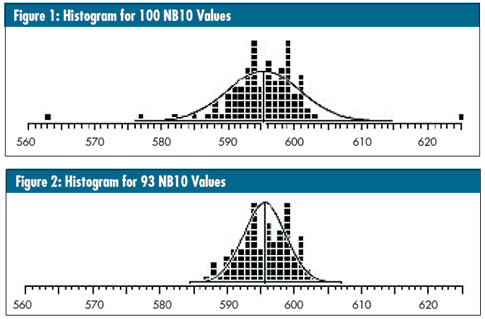
For example, the histogram in figure 1 has a bell-shaped curve superimposed. This curve is based on the average and standard deviation statistic for all 100 values in the histogram. It’s neither wide enough nor tall enough to provide a good fit to the data. The histogram in figure 2 contains the 93 values left after the seven extreme values (the four lowest and three highest) were deleted. Now the curve based on the average and the standard deviation statistic does a much better job of fitting the data. Thus, it’s true that outliers can undermine our efforts to create a model for our data.
…
Comments
Serious Series
or, as the hardcopy magazine says on page 18, "Removing the extreme values is always a series mistake."
Mistake? What mistake?
Yeah. We planned it that way. You see, they should be in a series... and uhhh... the outlier isn't in the series... so... it's a series mistake. See? Yeah, that's it.
Outliers!!!
Observations (or recorded data) is the only truth available to a researcher. It needs to be treated with respect, for it is for real. Models are a different species altogether. A researcher does not create/generate data to fit a model, rather the data represent the phenomenon under study as affected by the treatments and other controlled/uncontrolled all influencing factors. If an experimental data does not fit a generally considered appropriate model for the phenomenon, do not panic! The experimenter might be at the threshold of discovering something new, something that was probably not found earlier, so it is important. Or simply, the 'general model' was a result of 'censored data'. One experiments not to prove or otherwise a model, but try to honestly study a phenomenon the researcher has chosen to be of significance. Do not worry, if one is not able to give cogent explanations to the observations. Just state that. This will be much better than 'just censoring' the data.
The writeup by Donald Wheeler needs more material/explanation/further treatment. I do not know why he stopped at this brief explanation.
Nagin Chand
Scientist, CSIR and
former Adviser, AICTE
Add new comment