One-hundred-percent inspection is commonly used to avoid shipping nonconforming product. Each of the items produced is measured and judged to be either conforming or nonconforming. The conforming items get shipped, and the nonconforming items get set aside for use as factory-authorized replacement parts or some other equally ignominious fate. It all seems quite simple until you do the math. The purpose of this article is to show what happens when a product stream is subjected to 100-percent screening inspection with less-than-perfect measurement systems.
To simplify the mathematics, I will assume that the production process is being operated predictably, and that the stream of product values can be represented by our generic, worst-case probability model, the normal distribution. In our model we shall denote these product values by Y. In figure 1 we see the distribution of product values and the specifications for this product characteristic. This distribution represents the product stream, and when we measure an item, it is the value for Y that we are trying to determine.
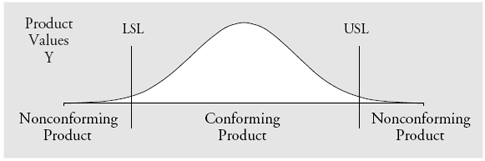
Figure 1: The distribution of the product values Y
…
Comments
Dealing with measurement uncertainty
This article addresses the real-world aspect of imperfect measurement systems instead of assuming the sterile textbook assumption that the measurement displayed by the gage is the actual dimension of the part. It's an important connection between gage R&R studies and the use of gages to ensure outgoing quality. I worked in an organization that called the practice of testing to artificially tightened specifications guardbanding; it protected the customer from borderline nonconforming product at the cost of rejecting borderline acceptable product.
Add new comment