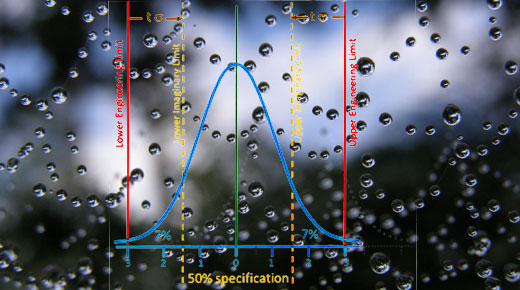
In my first article, the merits and cautions of AS9138 c=0 sampling plans were discussed and a simple formula was provided to determine the required sample size to detect nonconforming units. In the second article, the process control properties of MIL-STD-105 c>0 sampling plans were demonstrated, and the connectivity to other process control techniques was discussed. Here, a third alternative will be explored that applies the procedures of MIL-STD-105 to “imaginary limits” which are set proportionally inside the real “engineering specification.” This imaginary limit procedure thereby does not allow nonconforming units in the sample and has superior detection capabilities.

 …