Setting the Process Aim, Part 2

Making appropriate adjustments

Published: Monday, June 1, 2020 - 12:03

Setting the process aim is a key element in the short production runs that characterize the lean production of multiple products. Last month in part one we looked at how to use a target-centered XmR chart to reliably set the aim. This column will describe aim-setting plans that use the average of multiple measurements.

The necessity of process predictability

All effective aim-setting procedures will be built upon the notion of a process standard deviation. Some estimate of this process dispersion parameter will be used in determining the decision rules for adjusting or not adjusting the process aim. When a process is operated predictably this idea of a single dispersion parameter makes sense.

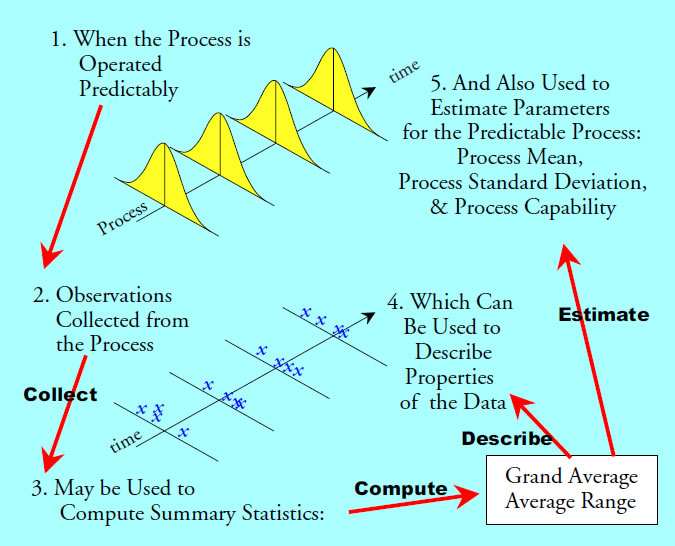
Figure 1: When statistics serve as estimates

When a process is operated unpredictably this idea of a single dispersion parameter evaporates. An unpredictable process can be thought of as having multiple personality disorder. It can change from one personality to another without warning. These personalities will have different averages and different standard deviations. While we may still compute a statistic for dispersion, it no longer can be said to be an "estimate" of anything.

Figure 2: When statistics are merely descriptive

There may be a never-ending need to "set the process aim" with an unpredictable process. But setting the process aim, as important as it may be, will not do anything to fix the underlying problem of the unpredictable process. Moreover, any changes in dispersion will undermine the procedures used to set the process aim.

Last month we used a target-centered XmR chart to set the process aim, and this process behavior chart provided a built-in check for process predictability. The procedures given below do not check for process predictability. They are meant to be used in conjunction with a process behavior chart, and they make use of the value of Sigma(X) provided by that chart. If this chart shows the process to be unpredictable, then you need to be looking for the assignable causes of the exceptional variation, rather than merely adjusting the process aim as the process upsets occur.  

The basic procedure and eight aim-setting plans

The basic procedure for setting the process aim is very simple:
1. Set the process aim.
2. Collect the specified number of measurements, n, and compute the average.
3. If this average is not within the decision interval [Target ± Delta], then return to step 1.
4. When the average falls within the decision interval, proceed with the production run, collecting data for the process behavior chart as appropriate.

Once operators have been given a consistent pair of values for n and Delta, they can use this procedure to set the process average as close to the target as is necessary, and they can do it quickly and efficiently.

The following aim-setting plans were developed for ease of use on the production floor. They all use a decision interval of the form [Target ± Delta] where Delta is a multiple of Sigma(X). As long as the average of a specified number of independent product measurements falls outside this decision interval, we will continue to make appropriate adjustments in the process aim. When the average falls within the decision interval, we cease adjusting the process aim.

Figure 3: Eight aim-setting plans

The judgment regarding what constitutes independent product measurements requires process knowledge. We do not want to collect the values so close together in time or space that they do not capture the routine process variation. Since it is futile to try to adjust the aim of an unpredictable process, and since the only way to avoid having an unpredictable process is to be using a process behavior chart, your experience with the process behavior chart will generally suffice both to provide the estimate of Sigma(X) needed and to establish how frequently to collect measurements for setting the process aim.

In order to know which of these plans to use, we need to look at how close to the target each plan will get the process average as well as the economic impact of using each plan. Remember the objective is to set the process aim so that the process average is close enough to the target value to result in a satisfactory production run.

How close does each plan get?

As described in part one, it is the posterior distribution for the average-to-target distance that tells us what we want to know about how a given aim-setting plan will work in practice. As we did there, by using a skeptical prior distribution for the possible values of the process mean, we can obtain conservative posterior distributions that are relatively independent of the prior distribution used. When we do this for each of the plans in figure 3, we end up with 95-percent upper bounds for the average-to-target distance. These upper bounds define what we can expect to get from each plan.

Aim-setting plan A: n = 1, Delta = 1.44 Sigma(X). Following each adjustment of the process aim, obtain n = 1 measurement from the process. When this value falls within the decision interval:

Target Value ± 1.44 Sigma(X)

the process average will be within 2.50 Sigma(X) of the target with a posterior probability of 0.95 or greater.

Aim-setting plan B: n = 3, Delta = 1.00 Sigma(X). Following each adjustment of the process aim, obtain n = 3 measurements from the process and compute their average. When this average falls within the decision interval:

Target Value ± 1.00 Sigma(X)

the process average will be within 1.55 Sigma(X) of the target with a posterior probability of 0.95 or greater.

Aim-setting plan C: n = 5, Delta = 0.75 Sigma(X). Following each adjustment of the process aim, obtain n = 5 measurements from the process and compute their average. When this average falls within the decision interval:

Target Value ± 0.75 Sigma(X)

the process average will be within 1.18 Sigma(X) of the target with a posterior probability of 0.95 or greater.

Aim-setting plan D: n = 10, Delta = 0.50 Sigma(X). Following each adjustment of the process aim, obtain n = 10 measurements from the process and compute their average. When this average falls within the decision interval:

Target Value ± 0.50 Sigma(X)

the process average will be within 0.82 Sigma(X) of the target with a posterior probability of 0.95 or greater.

 Aim-setting plan E: n = 15, Delta = 0.37 Sigma(X). Following each adjustment of the process aim, obtain n = 15 measurements from the process and compute their average. When this average falls within the decision interval:

Target Value ± 0.37 Sigma(X)

the process average will be within 0.64 Sigma(X) of the target with a posterior probability of 0.95 or greater.

Aim-setting plan F: n = 25, Delta = 0.25 Sigma(X). Following each adjustment of the process aim, obtain n = 25 measurements from the process and compute their average. When this average falls within the decision interval:

Target Value ± 0.25 Sigma(X)

the process average will be within 0.47 Sigma(X) of the target with a posterior probability of 0.95 or greater.

Aim-setting plan G: n = 40, Delta = 0.17 Sigma(X). Following each adjustment of the process aim, obtain n = 40 measurements from the process and compute their average. When this average falls within the decision interval:

Target Value ± 0.17 Sigma(X)

the process average will be within 0.36 Sigma(X) of the target with a posterior probability of 0.95 or greater.

Aim-setting plan H: n = 71, Delta = 0.10 Sigma(X). Following each adjustment of the process aim, obtain n = 71 measurements from the process and compute their average. When this average falls within the decision interval:

Target Value ± 0.10 Sigma(X)

the process average is within 0.25 Sigma(X) of the target with a posterior probability of 0.95 or greater.

Figure 4 summarizes these eight aim-setting plans.

Figure 4: Summary of eight aim-setting plans

Last month we found that the target-centered XmR chart would get the average-to-target distance below 1.14 Sigma(X) at least 95 percent of the time. So plans A and B are less effective than the target-centered XmR chart, and plan C is comparable to the target-centered XmR chart. Plans D and beyond will yield smaller average-to-target distances than the target-centered XmR chart.

So how close to the target do you need to be? Since the amount of data needed increases rapidly with the successive plans, it will help to understand the economic consequences of the possible choices.

How close do we need to be?

Because all aim-setting procedures will depend upon sample averages, they will all be less than perfect. We simply cannot get the process average (or mean) to be exactly the same as the target value. For this reason we have to settle for getting the process average close to the target. But how close is close enough? To answer this question, we shall use the concept of the effective cost of production. This cost is the nominal cost of production plus the excess costs of scrap and rework of nonconforming product, divided by the nominal cost of production: 

References one and two below show how the effective cost of production can be determined using both the capability ratio and the centered capability ratio. Since the cost of scrapping an item or a batch is logically greater than the cost of reworking it, we shall assume that all nonconforming product is scrapped as our worst-case scenario.

We shall also assume that the minimum amount of scrap, and therefore the minimum effective cost of production, will occur when the process is perfectly centered in the specifications (i.e., on target). As the process average drifts away from the target on either side, the scrap rate and the effective cost of production will increase.

For example, say we have a predictable process with a capability ratio of C_p = 0.60. When perfectly centered, this process can be expected to have an effective cost of production of 1.077. This means that the excess costs associated with the expected 7.2-percent scrap should amount to about 7.7 percent of the nominal cost of production. This is the best that can be expected from a process with a capability ratio of 0.60 when all nonconforming product is scrapped. The value of 1.077 is the minimum possible value for the effective cost of production for this process.

However, if this process is operated with a process average that is 0.54 Sigma(X) off-target, then it will have a centered capability ratio of:

 C_pk = [ C_p – 0.333 * (average to target distance in Sigma(X) units) ]
= [0.60 – (0.54/3)] = 0.42. 

Here the expected scrap rate would be 11.3 percent, and the effective cost of production would climb to 1.131. Since 1.131/1.077 = 1.050, we can say that operating this process with an average that is 0.54 Sigma(X) off-target increases the effective cost of production by five percent above the minimum possible effective cost of production. This ratio of the current effective cost of production to the minimum possible cost of production provides us with a way of summarizing the economic impact of operating off-target.

Since aim-setting procedures cannot get the process average exactly on target, we have to define some criterion to use in deciding that a process is reasonably close to the target. One economic criterion could be having an effective cost of production that is within 5 percent of the minimum possible effective cost of production. The curve in figure 5 shows those combinations of the capability ratios that correspond to this criterion.

Figure 5: The aim-setting region

The point shown on the curve is the example given in the above where C_p = 0.60 and C_pk = 0.42. The curve in figure 5 defines the left-hand boundary of the region where we want our processes to be after we have finished setting the process aim. When our capability indexes place our process to the right of this curve, the effective cost of production will be less than 105 percent of the minimum possible effective cost of production.

Choosing a plan

We know, for example, that plan A will get the average-to-target distance to be less than 2.50 Sigma(X) at least 95 percent of the time. So if we draw a horizontal line at the average-to-target distance of 2.50 Sigma(X) on figure 5, we know that plan A will get us below that line at least 95 percent of the time. 

If we look at the point where this horizontal line meets the aim-setting curve, we find that Plan A will get us in the aim-setting zone whenever the process capability ratio exceeds 1.39. Continuing in this manner, we find a set of minimum capabilities for each plan in figure 6.

Figure 6: Minimum capabilities for aim-setting plans

Criterion One

Say, for example, your process has a capability ratio of 0.80. Then from figure 6, the use of plan D to set the process aim will result in your process operating with an effective cost of production that is within 5 percent of its minimum effective cost of production with a probability of at least 95 percent. With a capability of 1.10, you could use plan B to operate within 5 percent of the minimum cost with a probability of 95 percent. So Criterion One for choosing a plan uses a 95-percent upper bound on the average-to-target distance. This makes figure 6 appropriate for those situations where the cost of scrap is substantial.

Figure 7: Criterion One for choosing a plan

By guaranteeing that the effective cost of production will be less than 105 percent of the minimum cost at least 95 percent of the time, Criterion One is a conservative guide. Most of the time your effective cost of production will be much smaller than 105 percent of the minimum cost. When we use the posterior probability distributions for the average-to-target distance along with the tables of the effective costs of production from reference one, we can compute the average effective costs of production for each plan. The curves in figure 8 show these average effective costs of production for each plan as a multiple of the minimum cost of production for that capability.

Figure 8: Average costs of production as a multiple of the minimum cost of production

Criterion One places you to the right of the arrow for each plan. As a result the arrows show the worst-case amounts for the ratio of the average cost of production to the minimum cost of production for each plan. The values corresponding to each arrow are listed in figure 9. 

Figure 9: Average costs of production when capabilities are at minimum

So while Criterion One gives us a 95-percent upper bound on the effective cost of production of no more than 105 percent of the minimum cost, it will, at the same time, result in average effective costs of production that are generally around 101 percent or less of the minimum cost.

Criterion Two

Figure 8 suggests the basis for alternative guidelines that would use smaller amounts of data in setting the process aim. If we are willing to let the average effective cost of production vary up to 102 percent of the minimum cost, then we could use the aim-setting plans with the alternative minimum capabilities of figures 10 and 11.

Figure 10: Criterion Two alternative capability minimums

Figure 11: Criterion Two for using aim-setting plans

Criterion Two will result in processes that, on the average, have an effective cost of production that is within 2 percent of the minimum. However, it will occasionally result in a process with an effective cost of production that exceeds 105 percent of the minimum cost. The advantage of Criterion Two over Criterion One is that, for a given capability, you will use fewer measurements following each adjustment. For example, with a process capability of 0.75, Criterion One calls for plan E, while Criterion Two calls for plan D. Thus, Criterion Two is useful in those cases where a lower cost of production makes setting the aim less critical than it is with Criterion One.

Criterion Three

If we are content to live with an average effective cost of production that is less than 103 percent of the minimum cost, then we can use the aim-setting plans with the minimum capabilities of figures 12 and 13.

Figure 12: Criterion Three alternative capability minimums

Figure 13: Criterion Three for using aim-setting plans

Criterion Three is useful for those processes where the nominal cost of production is very low. For a given capability, they will require fewer data following each adjustment of the process aim, and the average effective cost of production will be within 103 percent of the minimum possible cost. For our example of a process capability of 0.75, Criterion Three calls for plan C, rather than plans E or D as above.

These three criteria allow you to match the aim-setting plans to the particulars of your process. When nonconforming product is reworked, the lower cost of rework relative to scrap will also justify using Criterion Two or Criterion Three in place of Criterion One.

Summary

Eight aim-setting plans were presented along with three criteria for choosing between these eight plans. The criteria are based on the economic effect of each plan, and allow you to know what kind of outcome to expect from the use of each plan. Although the mathematics behind the criteria are complex, the plans are extremely easy to use in practice.

The three criteria allow you to use the process capability to choose a plan that will have certain outcome characteristics.

For comparison, the target-centered XmR chart from part one had a 95-percent upper bound on the average-to-target distance of 1.14 Sigma(X). What is the effect of using the target-centered XmR chart? When your process has a capability ratio of 0.80 or larger, the target-centered XmR chart will result in an average effective cost of production that is less than 103 percent of the minimum. This is roughly equivalent to plan C when used with Criterion Three in figure 13 above.

While other aim-setting plans could be devised, and while these plans would have different characteristics and outcomes, the plans given here have been proven to work satisfactorily in practice time and time again. Unlike problems in statistical inference, where proof beyond a reasonable doubt is required, the problem of setting the process aim only needs to get the process mean reasonably close to the target in order to result in a satisfactory production run. These plans allow you to do this with a minimum of effort.

Appendix one: notes on figure 4

Posterior probabilities have the form:

Probability of [State of Nature] given [Observed Outcome]

Here the observed outcome is the sample average falling within the decision interval, and the state of nature is the process mean being within the decision interval.

To compute these values, we have to begin with conditional probabilities of the form:

Probability of [Observed Outcome] given a [State of Nature]

These probabilities can be found in table 1 of reference five.

In order to convert conditional probabilities into posterior probabilities we have to use a prior probability model for the states of nature. Here I used traditional normal priors to model the uncertainty about the initial value for the process mean.

I computed the 95-percent upper bounds for the average-to-target distances using central intervals from the posterior distributions found using eight different priors. These priors ranged from very skeptical (probability mean in decision interval = 10%) to very gullible (probability mean in decision interval = 90%). Not surprisingly, the 95-percent upper bounds varied with the priors, but they stabilized with the skeptical priors. The values given in figure 4 came from the most skeptical priors and are the largest upper bounds found. Hence, the bounds given in figure 4 are conservative. In most cases the 95-percent central intervals will be tighter than these bounds, and the average-to-target distance will be smaller.

Appendix two: notes on figure 5

The computation of effective costs of production and their expression as a function of the capability ratios is explained in references one and two. These computations use a normal distribution to characterize the product stream because it is the distribution of maximum entropy, and as such it provides a worst-case scenario. Tables and formulas provided in reference one allow those who wish to do so to work out the relationship between the effective cost of production and the capability ratios using other probability models.

Appendix three: note on figure 8

An expanded version of tables one and two of reference one was created using increments in the average-to-target distance of 0.01 Sigma(X). Using the posterior probability distribution for each aim-setting plan expressed in increments of 0.01 Sigma(X) as weights, the weighted average of the effective costs of production across all average-to-target distances was found for each of the capability ratios shown in figure 7. These average effective costs of production were then divided by the minimum effective cost of production, and these ratios were plotted by plan and capability to obtain figure 8.

The posterior distributions used here came from neutral priors. I used neutral priors because here we are modeling the outcome of the final step in a multistep procedure. As each of the adjustments is made, we are presumably coming closer to getting the process mean near the target. While the posterior distributions for intermediate steps suggested gullible priors would be appropriate here, I used neutral priors in order to end up with conservative criteria for use.

References
1. Reducing Production Costs, Donald J. Wheeler, SPC Press, Knoxville, TN, 2010.
2. "The Effective Cost of Production and Use," Quality Digest, Aug. 2, 2010.
3. "The Gaps Between Performance and Potential," Quality Digest, Sept. 1, 2010.
4. "What is the Economic Zone of Production," Quality Digest, Oct. 4, 2010.
5. "Tables of the Power Function for Process Behavior Charts," Donald J. Wheeler and Rip Stauffer, available as a download at www.spcpress.com/pdf/DJW321.pdf.

About The Author

Donald J. Wheeler

Find out about Dr. Wheeler’s virtual seminars for 2023 at www.spcpress.com. Dr. Wheeler is a fellow of both the American Statistical Association and the American Society for Quality who has taught more than 1,000 seminars in 17 countries on six continents. He welcomes your questions; you can contact him at djwheeler@spcpress.com.