Why We Keep Having 100-Year Floods

Making predictions using historical data

Published: Monday, June 3, 2013 - 23:00

All data are historical. All analyses of data are historical. Yet all of the interesting questions about our data have to do with using the past to predict the future. In this article I shall look at the way this is commonly done and examine the assumptions behind this approach.

A few years ago a correspondent sent me the data for the number of major North Atlantic hurricanes for a 65-year period. (Major hurricanes are those that make it up to category 3 or larger.) I have updated this data set to include the number of major hurricanes through 2012. The counts of these major hurricanes are shown in a histogram in figure 1.

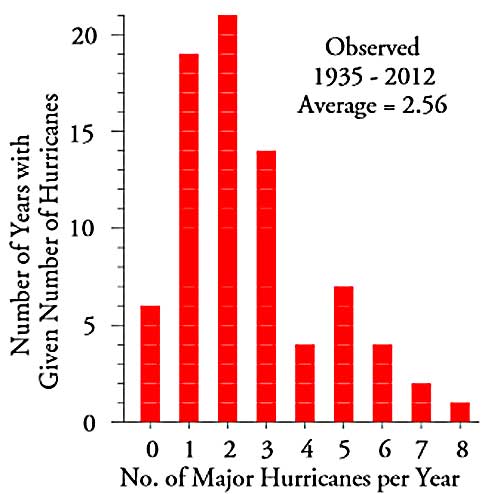
Figure 1: Histogram for the number of major North Atlantic hurricanes 1935–2012

A Poisson probability distribution is commonly used to model the number of hurricanes. Since the Poisson model only has one parameter, we only need to compute the average number of hurricanes per year to fit a Poisson distribution to the histogram of figure 1. The histogram shows an average of 2.56 major hurricanes per year. A Poisson distribution having an average of 2.56 is shown in figure 2.

Figure 2: The Poisson probability model with mean of 2.56

Using any one of several different test procedures, we can check for a lack-of-fit between the model in figure 2 and the histogram in figure 1. Skipping over the details, the result of these tests is that there is “no detectable lack of fit between the histogram and a Poisson model with a mean of 2.56.” Thus, it would seem to be reasonable to use the model in figure 2 to make estimates and predictions about the frequency of major hurricanes.

For example, we might decide to obtain an interval estimate for the average number of major hurricanes per year. In this case, an approximate 95-percent interval estimate for the mean number of major hurricanes per year is 2.2 to 3.0. 

Also, based on the model in figure 2, the probability of getting seven or more major hurricanes in any single year is 1.59 percent. This means that in any 78-year period we should expect to get about 78 × 0.0159 = 1.24 years with seven or more major hurricanes. Putting it another way, dividing 78 by 1.24, we find that a year with seven or more hurricanes should happen only about once every 63 years on the average. However, a glance at figure 1 shows that between 1935 and 2012 there have been three years with seven or eight major hurricanes. This is once every 26 years!

Well, perhaps we were simply too far out in the tail. Let’s look at how many years should have six or more major hurricanes. The Poisson model in figure 2 gives the probability of getting six or more major hurricanes in any single year as 4.61 percent. This means that in any 78-year period, we should expect to find about 78 × 0.0461 = 3.60 years with six or more major hurricanes. If we divide 78 by 3.60, we find that the model suggests we should have one year with six or more major hurricanes every 22 years on the average. 

In contrast to this, figure 1 shows that there have been seven years between 1935 and 2012 with six or more major hurricanes. Dividing 78 by 7, we find that we have actually had one year with six or more major hurricanes every 11 years on the average. Thus, we are having extreme years at twice the predicted frequency. Sound familiar?

So what is happening? Why do these data keep misbehaving? 

The first clue as to what is happening with these data can be found by simply plotting the data in a running record. When we do this, we immediately see that there are two different patterns of hurricane activity. In the periods before 1948 and from 1970 to 1994, there was an average of 1.49 major hurricanes per year. In the periods from 1948 to 1969 and after 1995, there was an average of 3.55 major hurricanes per year. During the periods of low activity, there could be up to four major hurricanes in a single year. During the periods of high activity, there could be up to 10 major hurricanes in a single year. These differences are reflected in the central lines and limits shown on the X chart in figure 3.

Figure 3: X chart for number of major North Atlantic hurricanes, 1935–2012. Click here for larger image.

To investigate this change in the weather patterns, I went to the NOAA website and found an article titled “NOAA Attributes Recent Increase in Hurricane Activity to Naturally Occurring Multi-Decadal Climate Variability” (Story 184). This article confirms the existence of the cycles shown in figure 3 and offers an explanation for this phenomenon. The histograms for these two levels of activity are shown in figure 4.

Figure 4: Histograms for the numbers of major North Atlantic hurricanes, 1935–2012

So what is wrong with the probability model used in figure 2? The problem is not with the choice of the model or with the mathematics, but rather with the assumption that the data were homogeneous. Anytime we compute a summary statistic, or fit a probability model, or do just about anything else in statistics, there is an implicit assumption that the data, on some level, are homogeneous. If this assumption of homogeneity is incorrect, then all of our computations, and all of our conclusions, are questionable. No single year between 1935 and 2012 is characterized by an average of 2.56 major hurricanes per year. Our 95-percent interval estimate of 2.2 to 3.0 major hurricanes per year simply does not apply to any year or any period of years. And our predictions as to how often certain numbers of major hurricanes will occur were completely off-base.

Yet this is what people are taught to do. The software makes it so easy to check for a lack of fit between a histogram and a probability model that many students have been taught elaborate systems for selecting and verifying a probability model as the first step in data analysis.

We collect data regarding all sorts of disasters: in addition to hurricanes, there are databases for tornadoes, floods, earthquakes, wildfires, etc. In each case we collect the observations into a single histogram, and use these observations to fit a probability model. It should be noted that when we do this, we are fitting the broad middle portion of the probability model to our data. Of course, this broad middle portion includes all of the commonly occurring events. If we fail to find a detectable lack of fit between our model and the observations, we will decide that we have the right model. Next we will then leave the broad middle of our probability model and move out into the extreme tails to make predictions about the frequency with which the more extreme events will occur: “According to the infinitesimal areas under the extreme tail of our assumed probability model, a flood of this magnitude will occur, on the average, only once in 100 years.” 

Of course, the model used for such a prediction is built on the assumption that the conditions that resulted in the more common events are the same conditions that result in the more extreme events. Since this assumption that the cause system remains the same is rarely correct, the data are rarely homogeneous. When the data are not homogeneous, the fitted model will be incorrect. When the fitted model is incorrect, our predictions will be erroneous. And when our predictions are erroneous, we end up having a 100-year flood about every 10 years or so.

This is why the primary question of statistical analysis is not, “What are the descriptive statistics?” Neither is it, “What probability model shall we use?” nor is it, “How can we estimate the parameters for a probability model?” The primary question of all data analysis is whether the data are reasonably homogeneous. When the data are not homogeneous, the whole statistical house of cards collapses. Hence, Shewhart’s Second Rule for the presentation of data: “Whenever an average, range, or histogram is used to summarize the data, the summary should not mislead the user into taking any action that the user would not take if the data were presented as a time series.” 

The primary technique for examining a collection of data for homogeneity is the process behavior chart. Any analysis of observational data that does not begin with a process behavior chart is fundamentally flawed.

About The Author

Donald J. Wheeler

Dr. Wheeler is a fellow of both the American Statistical Association and the American Society for Quality who has taught more than 1,000 seminars in 17 countries on six continents. He welcomes your questions; you can contact him at djwheeler@spcpress.com.