Lean production is built on the explicit assumption that each step is operated predictably and capably. Predictable operation can only be achieved and maintained by using process behavior charts. But short production runs and multiple products make it hard to see how to use process behavior charts in a lean environment. So what can be done? This paper will show how to use a zed chart for individual values to track your process while it is making different products.

Unit 12

Unit 12 is used to make Products 1201 and 1202. The final characteristic for Product 1201 has a target value of 19.0, while the final characteristic for Product 1202 has a target value of 8.0. Batches 43 through 72 contain short runs of both products.

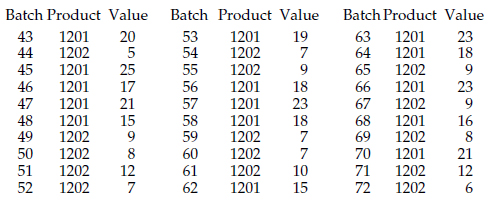
Figure 1: Data for Unit 12

Of course a naive approach would be to simply place the data from Unit 12 on an XmR chart as shown in figure 2.

 …