The ability to make predictions has always been rewarded. Statistician Donald J. Wheeler says that “prediction is the essence of business.” With growing bodies of data and good analytical models, our predictions are getting better.
|
ADVERTISEMENT |
The statistical models and algorithms behind prediction can be intimidating. Topics such as regression and neural networks can make the methods of prediction seem out of reach. However, a control chart—a simple statistical process control tool—can put the power of useful prediction within your grasp.
Consider the following data series:
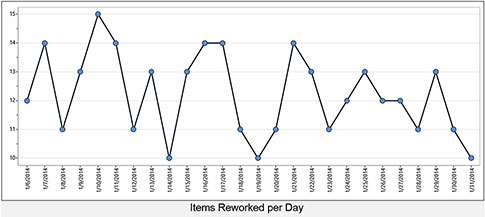
Click here for larger image.
When presented in this form, what kind of predictions can you make about the response variable? You might note the scale of the chart and make this prediction:
Most of the data will be between 10 and 15.
…
Comments
More Analysis Needed
Thanks for your article explaining the use of Process Behavior Charts. However, the analysis needs to go a few steps farther. In your final chart, the parameters of UCL, LCL, and Mean are meaningless in this context. The first three data points and the last 17 points appear to come from the same process, while the data for 3/18 - 3/23 suggest a definite upset in the system. I suggest you replot the chart with centerlines and control limits for each of these populations, easily done with most software. Then, what lesson(s) can be learned from studying the points of 3/18 - 3/23? What happened? The true underlying process may be centered at 11.0 - 11.5. Obviously, the desired number of reworked items per day is zero, but the process "knows" NOTHING of your wants and desires (i.e., specs)! Next, one could work on the process and determine if the process goes "out of control" to the low side as a result.
Add new comment