There are many tools available for investigating quality problems. One useful and easy-to-use set of statistical tools is John W. Tukey’s exploratory data analysis (EDA), which quality engineers can use for generating hypotheses. Tukey’s EDA provides many different methods for looking at data, and the hypotheses generated using EDA can lead to the root cause of quality problems.

In his book Exploratory Data Analysis (Pearson, 1977), Tukey recommends EDA for exploring data and uncovering evidence that can later be confirmed through conformation testing. This is especially useful when seeking the root cause of quality failures or the reason a process isn’t performing optimally.

With EDA, graphical methods are used to display data with the objective to explore and gain insight into a data set. An optimal time to use EDA is at the start of a root cause analysis. Data should be collected and then subjected to EDA methods to form a preliminary hypothesis, which can then be confirmed by using other statistical methods such as hypothesis testing, regression analysis, analysis of variance (ANOVA), or nonparametric tests.

Tukey used precipitation in New York City to illustrate the use of box plots, and this article will take his idea a step further and use precipitation in the state of New York to demonstrate the use of the EDA tools for root cause analysis.

The data set contains the yearly amount of precipitation in the state of New York between 1886 and early 2013; the precipitation data were rounded to the nearest inch.

The stem-and-leaf diagram depicted in figure 1 was created by entering the data into Minitab Statistical Software. A stem-and-leaf diagram graphically depicts the shape of a distribution while still maintaining the original values. The tens value is in the stem column (second column in figure 1), and the ones values are in the leaf column (third column). A ones digit is shown for each time that value appeared in the data series. So in the case of 30, 30, 30, 31, the stem would be 3, and the leaf would be 0001. For our data set, the stem-and-leaf diagram shows the majority of results were clustered around 38 in. and 39 in. of rain, as shown in figure 1.  

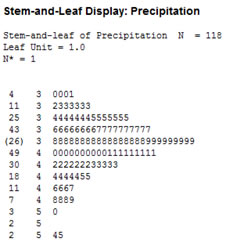
Figure 1: Stem-and-leaf diagram of precipitation in New York state from 1886–2013

The data were then entered into a dot plot, which uses dots in place of bars and allows the visualization of the individual data points. The dot plot depicted in figure 2 shows the concentration of results around 38 in., with a few potential outliers at almost 56 in. The same data can be seen in the histogram in figure 3.

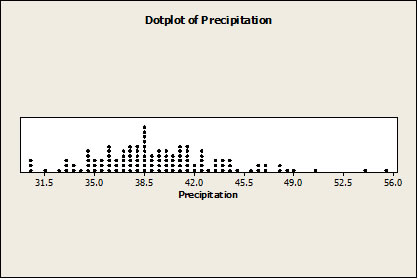
Figure 2: Dot plot showing concentration of precipitation

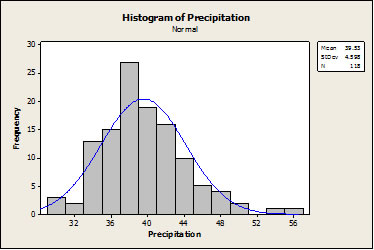
Figure 3: Histogram showing concentration of precipitation

Like the stem-and-leaf diagram and dot plot, the histogram shows the spread of the data with a concentration around 38 in. and several outliers on the high side. A quality engineer could quickly observe the spread of the data by using a stem-and-leaf diagram, dot plot, or histogram.

In all three of these graphical displays, the skew of the data is quickly observable, but these may not present a complete picture. All we can see is the range and distribution of rainfall over time. Interesting, but not very useful. In order to gain more insight, we need to enter the data into a time series plot to look for potential patterns.

The time series plot of precipitation in figure 4 shows an increase in precipitation over time. The average of any given year varies; therefore, some years during the 1990s had less rain than years during the 1890s, but a trend appears to be present and is even more noticeable when the data are separated into groupings of 19 years each and then entered into the box plot in figure 5.

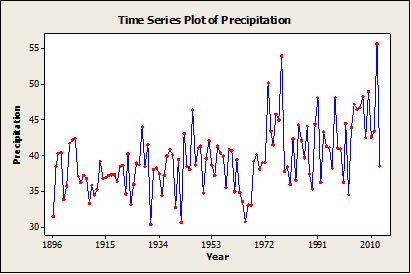
Figure 4: Time series plot of precipitation

Box plots, also known also box-and-whisker diagrams, are a simple yet effective part of EDA. They can easily be constructed by hand or by using a statistical software program. The box in the box plot contains the 25th and 75th percentiles and uses a horizontal line within the box to identify the median of the data set. The average of the data set is identified by a plus sign with a circle around it. The lines, or whiskers, identify the rest of the data set, except when outliers are present. Outliers, which are numbers that deviate greatly from the rest of the data set, are identified by asterisks.

The box blot in figure 5 shows that the range of the data has increased during the past four decades as compared to earlier data. It would also appear that New York state has gotten wetter during the past 40 years. (The final grouping is an exception; however, only a few years’ worth of data was used for this grouping.)  

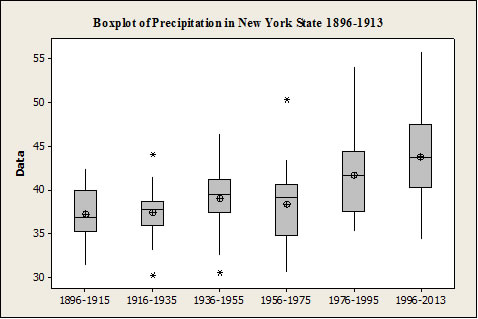
Figure 5: Box plot of precipitation in New York state from 1896–2013

Any one of the EDA concepts could have yielded clues and all four methods wouldn’t have been necessary for an actual root cause analysis. If the data had been from a manufacturing process, a quality engineer could have quickly gained a basic understanding of the data set by using a box plot or dot plot, followed by a time series plot.

The same EDA concepts could have been used by a quality engineer analyzing the dimensions of a manufactured product. For example, a quality engineer might collect data on the diameter of a machined cylinder during a root cause analysis. The data could then be subjected to EDA to gain a basic understanding of what’s happening during the processes, and this could then be subjected to methods of a more quantitative nature. Figure 6 depicts a two-sample t-test of the New York state precipitation data. The null hypothesis looked at the amount of precipitation between 1896 and 1905 and is equal to the precipitation between 1996 and 2013. The alternative hypothesis looked at whether there is a difference between the two time periods.

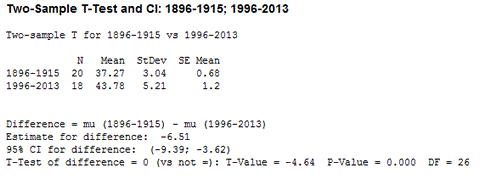
Figure 6: Two-sample t-test showing precipitation in New York state

Tukey’s EDA was used to observe the data set and find a potential hypothesis that was later confirmed through a more concrete method. Had this been cylinder diameter data, a quality engineer could conclude that the mean is increasing over time based on the hypothesis test. After this, the quality engineer could begin investigating the root cause for the increase in the cylinder diameter.

Originally published February 2014 in a modified form on the German website www.QZ-Online.de as “Die explorative Datenanalyse nach Tukey.”