Right Chart or Right Action?

No extra credit for choosing the technically correct chart

Published: Wednesday, June 11, 2014 - 14:52

Do you still insist on asking, “Which chart do I use for which situation?”

I’ve seen many flowcharts in books to help you answer this question. They’re all some variation of this:

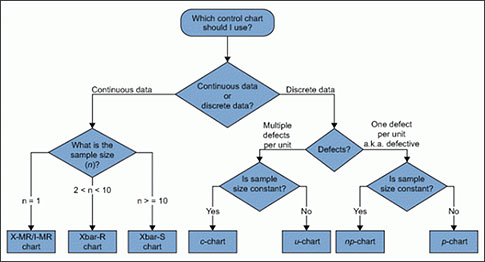
I find them far too confusing for the average user and have never taught this in my work. Besides, you get no credit for choosing the technically correct chart or computing the right numbers—only for taking the right action.

Your ‘Swiss Army knife’

For any initial chart for process assessment, the data should be in its naturally occurring time sequence, preferably as a run chart. Next, the control chart of choice with which to start is virtually almost always the I-chart (individuals chart), which uses the moving range (MR) between consecutive points to determine its common-cause limits. The I-chart is the “Swiss Army knife” of control charts. As I have discovered time and time again, it usually approximates the “correct” chart under most conditions, and its use is easier to explain.

I can hear the chorus: “So, what are the conditions when it isn’t correct?”

Bottom line: Before you ask me, “Which chart should I use for which situation?” or challenge me with a “what if” doomsday scenario (I’m truly amazed at the creative hypothetical situations thrown at me during my teaching), let me request that you use a sequence which by now should seem awfully familiar:
1. Could you please show me the data (or describe an actual situation) that are making you ask me this question?
2. Please tell me why this situation is important.
3. Please show me a run chart of this indicator plotted over time.
4. What ultimate actions would you like to take with these data?

If you have the patience to answer these, and follow them through with a data set to reach an appropriate action, you will probably have answered the question yourself—and solved a major problem in the process—while saving yourself a major side trip into the swamp of calculation minutiae.

Note: In some of the figures mentioned above, it is advertised as an I-MR chart combination. Don’t worry too much about the MR chart for the moment. Your main concern with that chart is its easily calculated upper limit, which gives you the maximum value by which two consecutive data points can differ randomly.

And then there remains (still) the problem of getting the limits right. In my searches, I was amazed at how many said to calculate the standard deviation (as we were taught in basic statistics) and multiply it by three to get the limits around the average. What part of “never” don’t people understand?

So let’s consider the various other charts.

C-charts (for counts)

C-charts are easily approximated by the I-chart, especially if the average of the data is at least five. Remember, the process’s stability is actually the key question and determines whether you subsequently use a common- or special-cause strategy.

Small numbers (and rare events) can get very tricky and usually require guidance by a statistical expert to get the right number. Although, in the troublesome case of rare events, plotting the time between occurrences of them can be useful... as an I-chart.

Regardless, the run chart and I-chart will generally lead you to the right initial action.

P-charts and u-charts

When p-charts (percentages) and u-charts (rates) are plotted over time, pretty much everyone gets confused by the stair-step limits caused by the varying denominator sizes. This confusion only escalates by well-meaning attempts to explain them. Occasionally, the chart might come in handy for finding an individual outlier.

More important, these become problematic, especially p-charts, when data are aggregated monthly or quarterly or even annually. The resulting large denominators (as in hundreds or thousands) artificially create many out-of-control signals (above or below the limits).

At the opposite extreme, p-charts also get tricky if you have very small denominators, which is true for the I-chart as well. Sometimes, one needs to aggregate subgroups to smooth things out a bit.

Donald Wheeler is of the opinion that the assumption of true independence of occurrence of events necessary for proper use of a p-chart is rarely encountered in reality. He feels it is correct to use only the I-chart. My experience has pretty much borne this out. (Wheeler’s books are very practical and well-written with good examples. You can peruse them here.)

All that said, I have found p-charts and u-charts to be helpful in stratification (a common cause strategy). One uses them to compare, statistically, individual rates that, ideally, each have been obtained by:
1. Plotting a run chart
2. Following up with a control chart
3. Determining the most recent stable history
4. And then and only then aggregating the data obtained from 3) into summed numerators and denominators for statistical comparison.
5. Then use a p-chart analysis of means to expose special causes for subsequent focus.

In these cases, the horizontal axis is not time; for example, it could be a comparison of individual doctors or locations.

Many of you have no doubt encountered these via the fancy euphemism “funnel plots,” where the results are sorted horizontally by lowest to highest denominator size, creating a funnel-like shape of common cause.

X-bar/R charts and X-bar/S charts

For healthcare readers, I’ll tell you right now: You virtually never use these. They were designed for manufacturing processes where thousands of parts are made per day, and it’s no big deal to grab, say, four to five parts, produced consecutively, every hour (which takes seconds). People—even at manufacturing facilities—seem to find these confusing and hard to use because the limits are based on the behavior of averages, not the individual parts. And the plague of putting specification limits on these charts (which is wrong, wrong, wrong... what part of “never”...?) continues, which causes a specification focus, not a process focus.

In healthcare clinical applications, you don’t have patients coming through in numbers similar to an assembly line. I literally can’t remember the last time I’ve used these charts in my healthcare work—and that’s over the course of 20 years. They might lend themselves to high-volume administrative processes, but, once again, people will still find them confusing.

So, I never formally teach them and would do so only if needed in the context of solving an issue.

Np-chart

As far as the np-chart goes, it’s a marginal pedagogical classroom exercise, and that’s about it. I virtually never use one because having equal sample sizes in the denominator is a rare luxury indeed. Or, the machinations to create equal denominators and then explain the resulting chart to one’s puzzled audience far outweighs any benefits.

Always start with process data gathered over time, and plot a run chart

First, find out what you’re “perfectly designed” to get and, second, see whether common and/or special cause strategies are needed to further solve the problem. Also, this gives you a baseline with which to assess the current state as well as your subsequent intervention efforts.

Many projects fail because they lack a baseline. So you see, there is never an escape from plotting your process data over time.

And if you insist on picking the right chart, be my guest. Here is an inventory I encountered on one website (without a flowchart to help you). This list includes neither the multivariate ones I encountered on a search, nor the one I found based on the Mann-Whitney statistic.

Correct chart or correct action? Until next time....

About The Author

Davis Balestracci

Davis Balestracci is a past chair of ASQ’s statistics division. He has synthesized W. Edwards Deming’s philosophy as Deming intended—as an approach to leadership—in the second edition of Data Sanity (Medical Group Management Association, 2015), with a foreword by Donald Berwick, M.D. Shipped free or as an ebook, Data Sanity offers a new way of thinking using a common organizational language based in process and understanding variation (data sanity), applied to everyday data and management. It also integrates Balestracci’s 20 years of studying organizational psychology into an “improvement as built in” approach as opposed to most current “quality as bolt-on” programs. Balestracci would love to wake up your conferences with his dynamic style and entertaining insights into the places where process, statistics, organizational culture, and quality meet.