Estimating the Fraction Nonconforming

How to know what the data are really telling you

Published: Tuesday, May 31, 2011 - 11:03

Whenever we present capability indexes the almost inevitable follow-up question is, “What is the fraction nonconforming?” What this question usually means is, “Tell me what these capability indexes mean in terms that I can understand.” These questions have resulted in multiple approaches to converting capability indexes and performance indexes into fractions nonconforming. This article will review some of these approaches and to show their assumptions, strengths, and weaknesses.

The empirical approach

In order to make the following discussion concrete, we will need an example. We shall use a collection of 100 observations obtained from a predictable process. These values are the lengths of pieces of wire with a spade connector on each end. These wires are used to connect the horn button on a steering wheel assembly. The upper specification for this length is 113 mm.

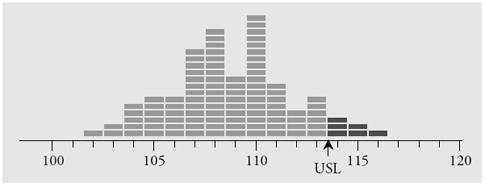
Figure 1: Histogram of 100 wire lengths

The oldest and simplest approach to estimating the fraction nonconforming is arguably the best approach. Here the estimate of the fraction nonconforming is simply the number of observed values that are outside the specifications, Y, divided by the total number of observed values, n. The name commonly used for this ratio is the “binomial point estimate”:

This ratio provides an unbiased estimate of the process fraction nonconforming. For the data of figure 1, the specifications are 97 mm to 113 mm. Six of the observed values exceed 113, so Y = 6, n = 100, and our binomial point estimate for the fraction nonconforming is p = 0.06 or 6 percent. Note that the reference to the binomial distribution does not apply to the wire lengths, X, but rather to the counts Y and n. This approach makes no assumptions regarding the histogram in figure 1. No probability model is assumed. No lack-of-fit tests are used. Just count how many values are outside the specifications and divide by the total number of observed values.

If the data come from 100-percent inspection, then there is no uncertainty in the descriptive ratio above. The 6 percent is the fraction rejected at inspection, and the only uncertainty is the uncertainty of misclassification, as described in my column last month. However, if we are using the data of figure 1 for representation or prediction, then we will have to be concerned with the uncertainty involved in the extrapolation from the product measured to the product not measured. In this case the production process was being operated predictably, so this extrapolation makes sense. (To read more about representation and prediction see my April column, “How Measurement Error Affects the Four Ways We Use Data.”)

When data are used for representation or prediction, we will need to use an interval estimate in addition to the point estimate. The interval estimate will define the range of values for the process fraction nonconforming that are consistent with the observed point estimate.

Most textbooks will give a formula for an approximate 95-percent interval estimate that is centered on the binomial point estimate p:

This formula was first given by French mathematician Pierre Simon Laplace in 1812 and is today commonly referred to as the “Wald interval estimate.” Although this simple approximation is satisfactory when the proportions are in the middle of the range between 0.00 and 1.00, it does not work well for proportions that are close to either 0.00 or 1.00. Since the fraction nonconforming will hopefully be near 0.00, we will need to use a more robust interval estimate given by E. B. Wilson in 1927. The 95-percent Wilson interval estimate will be centered on a value known as the “Wilson point estimate”:

This Wilson point estimate effectively shifts the center of the interval estimate so that the formula will yield a more appropriate interval. Using Y = 6 and n = 100, the Wilson point estimate is 0.0769, and the 95-percent Wilson interval estimate for the process fraction nonconforming is:

So using the specifications above, the data in figure 1 give us a binomial point estimate of 6 percent, and a 95-percent Wilson interval estimate for the process fraction nonconforming of 2.6 percent to 12.8 percent. While 6 percent nonconforming is our best point estimate, the uncertainty of the extrapolation from our observed values to the underlying process means that our observed value of 6 percent nonconforming is consistent with a process that is producing anywhere from 2.6 percent to 12.8 percent nonconforming.

If we changed the upper specification to be 114 mm, then Y would be 3, the binomial point estimate would be 3 percent, and the 95-percent Wilson interval estimate would be 0.0481 ± 0.0411. Thus, an observed value of 3 percent nonconforming would be consistent with a process fraction nonconforming of 0.7 percent to 8.9 percent.

Now consider what would happen if the upper specification was 116 mm. Here Y would be 0, the binomial point estimate would be 0 percent, and yet the 95-percent Wilson interval estimate would be 0.0192 ± 0.0264. Thus, our observed value of 0.0 percent nonconforming would be consistent with a process fraction nonconforming of 0.0 percent to 4.6 percent. Since Y can not get any smaller than zero, this last interval estimate reflects the limitations of the inferences that can be drawn from 100 observed values. Processes producing less than 4.6 percent nonconforming can, and will, produce some 100 piece samples that have zero nonconforming items!

Thus, the Wilson interval estimate provides us with a way to characterize the process fraction nonconforming based on the observed fraction nonconforming. It defines the uncertainty that is inherent in any use of the data to estimate the process fraction nonconforming.

The probability model approach

Sometimes, rather than using the data to directly estimate the fraction nonconforming, a probability model is fitted to the histogram and used to compute the tail areas beyond the specification limits. While the data are used in fitting the probability model to the histogram, the estimate of the fraction nonconforming will be obtained from the fitted model rather than the data. As an example of this approach we will fit a normal distribution to the wire length data from figure 1.

Figure 2: A normal distribution fitted to the wire length data

The wire length data have an average of 109.19 mm, a standard deviation statistic of 2.82 mm, and the process behavior chart shows no evidence of unpredictable operation while these values were obtained. A normal probability model having a mean of 109.19 and a standard deviation parameter of 2.82 is shown superimposed on the histogram in figure 2. As before, we begin with the assumption that the upper specification limit is 113 mm. In the continuum used by the model, this becomes 113.5 mm. When we standardize 113.5 mm, we obtain a z-score of 1.53, and from our standard normal table we find that this corresponds to an upper tail area of 0.0630. Thus, using a normal probability model we obtain a point estimate of the process fraction nonconforming of 6.3 percent, which is not much different from the empirical estimate found earlier.

So, just how much uncertainty is attached to this estimate? Judging from the few cases where the formulas for interval estimates are known, we can say that if the probability model is appropriate, then this estimate is likely to have a slightly smaller interval estimate than the empirical approach. However, if the probability model is not appropriate, then this estimate can have substantially more uncertainty than the empirical estimate. Which brings us to the first problem with this approach: Any choice of a probability model will, in the end, turn out to be an unverifiable assumption. It amounts to nothing more than an assertion made by the investigator.

While lack-of-fit tests may sometimes allow us to rule out a probability model, no test will ever allow us to validate a particular probability model. Moreover, given a sufficient amount of data, you will always detect a lack of fit between your data and any probability model you may choose. This inability to validate a model is the reason that it is traditional to use the normal distribution when converting capabilities into fractions nonconforming. Since the normal distribution is a maximum entropy distribution, its use amounts to performing a generic, worst-case analysis. (It is important to note that this use of a normal distribution is a matter of convenience, arising out of a lack of information, and is not the same as an a priori requirement that the data “be normally distributed.”)

To illustrate the generic nature of estimates based on the normal distribution, we will use the ball-joint socket thickness data shown in figure 3. There we have 96 values collected over the course of one week while the process was operated predictably. The average is 4.667, and the estimated standard deviation is 1.80.

The first probability model fitted to these data is a normal distribution having a mean of 4.667 and a standard deviation parameter of 1.80. There is a detectable lack of fit between the histogram and this normal distribution.

The second probability model fitted to these data is a Burr distribution with c = 1.55 and k = 58.55 that has been shifted to have a mean of 4.667 and stretched to have a standard deviation parameter of 1.80. There is no detectable lack of fit between this Burr distribution and the histogram.

Figure 3: Two probability models fitted to the socket thickness data

When working with skewed histograms like the one in figure 3, we are primarily concerned with areas in the long tail because the short tail is usually restricted by a barrier or boundary condition. Considering the discrete values found in these data we will consider the upper tail areas defined by the cutoff values of 5.5, 6.5, 7.5, etc. The table in figure 4 shows these upper tail areas computed three ways: (1) using the normal distribution, (2) using the fitted Burr distribution, and (3) using the empirical binomial point estimate. Finally, the last two columns in figure 4 give the lower and upper bounds for the process fraction nonconforming based on the 95-percent Wilson interval estimates.

Figure 4: Three different estimates of upper tail areas

As expected, the estimates based on the normal probability model differ from those found using the Burr probability model. Moreover, these estimates also differ from the binomial point estimates shown in the third column. However, in each row, all three estimates fall within the bounds defined by the 95-percent Wilson interval estimate. This illustrates what will usually be the case: The uncertainty inherent in the data will usually be greater than the differences between the various estimates.

This makes any discussion about which estimate is best into a mere argument about noise. When we are estimating the fraction nonconforming, the uncertainty in our estimates will generally overwhelm the differences due to our choice of probability model. The numbers you obtain from a probability model are not really as precise as they look. And that is why the generic ballpark values obtained by using a normal distribution will usually be sufficient. (Remember, the normal distribution displayed a detectable lack of fit for these data, and yet all of the normal estimates fell within the intervals defined by the uncertainty in the empirical estimates.)

“But using a fitted probability model will let us compute tail areas for capability indexes greater than 1.00,” you say.

Yes, it will, and that is the second problem with the probability model approach. No matter how many data you have, there will always be a discrepancy between the extreme tails of your probability model and the tails of your histogram. This happens simply because histograms always have finite tails while probability models usually have at least one infinite tail. The table in figure 5 shows the average size of the finite tails of a histogram. There I have listed the average distances between the average of a histogram and the maximum value for that histogram. These distances are given in standard deviation units.

Figure 5: Histogram tails grow very slowly with increasing n

Once you get beyond 200 data, the tails of the histogram grow ever more slowly with increasing amounts of data. While most of the values in figure 5 have been known since 1925, this aspect of data analysis has seldom been taught to students. These values show that the major discrepancies between a probability model and a histogram are generally going to occur in the region out beyond three standard deviations on either side of the mean. Call this region the extreme tails of the probability model. When we are converting capability indexes that are less than 1.00 into a fraction nonconforming, these discrepancies in the extreme tails between our histogram and our probability model will not have much of an impact. (Six percent nonconforming plus or minus 60 parts per million is still 6 percent nonconforming.)

But, when your capability indexes get to be larger than 1.00, any conversion will require the computation of infinitesimal areas under the extreme tails of the assumed probability model. Here small differences in the probability model can result in dramatic changes in the computed values. (Sixty parts per million plus 60 parts per million will be 120 parts per million.) To illustrate this, figure 6 will extend the table of figure 4 to cutoff values beyond three sigma. Here the upper tail areas are given in parts per million:

Figure 6: Estimating extreme upper tail areas

The upper specification limit for the socket thickness data is 15.5. Which estimate from figure 6 should you tell your boss? 1 ppb? 24 ppm? Or something less than 4.7 percent?

When we get beyond three sigma we find considerable differences between the upper tail areas of the two different probability models. At the upper specification cutoff of 15.5, these areas differ by a factor of 24,000. However, all 18 estimates in figure 6 are estimates of a process fraction nonconforming that, according to the data, falls somewhere between 0 percent and 4.7 percent. While our assumed probability models allow us to compute numbers out to parts per million and parts per billion, the data themselves will not support an estimate that is more precise than to the nearest five parts per hundred. Think about this very carefully.

When you compute tail areas out beyond three sigma, you are computing values that are entirely dependent upon the assumed probability model. These tail areas will have virtually no connection to the original data. Because of the inherent discrepancy between the tails of the histogram and the tails of the probability model, converting capability indexes that are larger than 1.00 into fractions nonconforming will tell you more about the assumed model than it will tell you about either the data or the underlying process. This is why such conversions are complete nonsense.

Thus, there are two problems with using a probability model to estimate the process fraction nonconforming. The first is that any choice of a probability model is essentially arbitrary, and the second is that the use of a probability model encourages you to extrapolate beyond the tails of the histogram to compute imaginary quantities.

Given the uncertainty attached to any estimate of the process fraction nonconforming, the choice of a probability model will usually make no real difference as long as the capability indexes are less than 1.00. Here the use of a generic normal distribution will provide reasonable ballpark values, and there is little reason to use any other probability model.

However, when the specifications fall beyond the tails of the histogram, and especially when the capability indexes exceed 1.10, no probability model will provide credible estimates of the process fraction nonconforming. Computing an infinitesimal area under the extreme tails of an assumed probability model is an exercise that simply has no contact with reality.

The histogram shows us what we know, and it also reveals what we do not know. When we add an assumed probability model to our histogram we are adding ink that does not represent the data. The technical term for such nondata-ink is “chartjunk.” Like a stage magician’s props, this chartjunk serves to distract our attention from the reality of the histogram and to usher us into the realm of illusion and make-believe.

Figure 7: The difference between chartjunk and data

So what do we really know?

What we know depends upon how many data we have and whether or not those values were collected while the process was operated predictably. Moreover, the only way to determine if the data were obtained while the process was operated predictably is by using a process behavior chart with rational sampling and rational subgrouping.

If the data show evidence that the process was changing while the data were collected, then the process fraction nonconforming may well have also changed, making any attempt at estimation moot. (In the absence of a reasonable degree of predictability, all estimation is futile.)

If the data show no evidence of unpredictable operation, then we may use the binomial point estimate to characterize the process fraction nonconforming. In addition we may also use the 95-percent Wilson interval estimate to characterize the uncertainty in our point estimate. This approach is quick, easy, robust, and assumption free.

When no observed values fall beyond a specification limit, our count Y becomes zero and the binomial point estimate goes to zero. However, the 95-percent Wilson interval estimate will still provide an upper bound on the process fraction nonconforming. These upper bounds will depend solely upon the number of observations in the histogram, n. Selected values are shown in the table in figure 8.

Figure 8: The uncertainty in estimates of fractions nonconforming when Y = 0

The upper bounds listed in figure 8 define the essential uncertainty in all estimates of the fraction nonconforming that correspond to Y = 0. This means that when you use a probability model to compute a tail area that is beyond the maximum or the minimum of your histogram, then regardless of the size of your computed tail area, the process fraction nonconforming can be anything up to the upper bound listed in figure 8. There we see that it takes more than 1,000 data to get beyond the parts-per-hundred level of uncertainty.

Say, for example, that you have a histogram of 70 data collected while the process was operated predictably and on-target with an estimated capability ratio of 1.33. Say that these data are suitably bell-shaped and that you use a normal distribution to estimate the process fraction nonconforming to be 64 parts per million. Figure 8 tells us that with only 70 data, all you really know about the process fraction nonconforming is that it is probably less than 6.4 percent nonconforming. This is 1,000 times the computed value of 64 ppm! With this amount of uncertainty, how dogmatic should you be in asserting that the process fraction nonconforming is 64 parts per million?

Until you have hundreds of thousands of data collected while the process is operated predictably, you simply do not have any basis for claiming that you can estimate the fraction nonconforming to the parts-per-million level.

One day a client from a telephone company observed that they computed the number of dropped calls each day in parts per million. However, in this case they were using the empirical approach and the denominator was in the tens of millions. With this amount of data the uncertainty in the computed ratio was less than 0.5 ppm, and reporting this number to the parts-per-million level was appropriate.

But for the rest of you, those who have been using a few dozen data, or even a few hundred data, as the basis for computing parts-per-million nonconforming levels, I have to tell you that the numbers you have been using are no more substantial than a mirage. The uncertainties in such numbers are hundreds or thousands of times larger than the numbers themselves.

The first lesson in statistics is that all statistics vary. Until you understand this variation, you will not know the limitations of your computed values. Using parts per million numbers based on a few hundred data without regard to their uncertainties is a violation of this first lesson of statistics and is a sign of a lack of understanding regarding statistical computations.

About The Author

Donald J. Wheeler

Dr. Wheeler is a fellow of both the American Statistical Association and the American Society for Quality who has taught more than 1,000 seminars in 17 countries on six continents. He welcomes your questions; you can contact him at djwheeler@spcpress.com.