There are two basic ideas or principles that need to be respected when creating a chart for individual values and a moving range (an XmR chart). This column will explain and illustrate these two principles for effective XmR charts.

The first principle for an effective XmR chart is that successive values need to be logically comparable. The second is that the moving ranges need to isolate and capture the local, short-term, routine variation that is inherent in the data. When these principles are ignored, the XmR chart can miss signals that it would otherwise detect.

While the use of the time-order sequence of the data will usually be sufficient to satisfy these two principles, there are times when a careful consideration of the context for the data will require a different organization. As a case in point consider the camshaft bearing diameters shown in figure 1. The strict time-order for these data is:

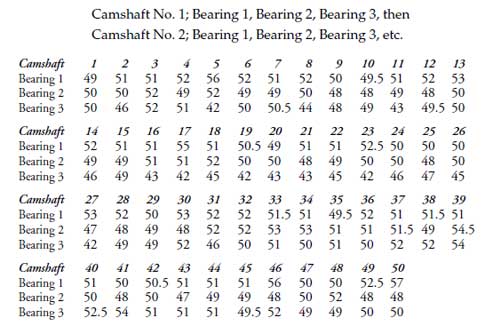
Figure 1: The camshaft bearing diameters

 …