Photo by Scott Graham on Unsplash
Clear thinking and simplicity of analysis require concise, clear, and correct notions about probability models and how to use them. Here, we’ll examine the basic properties of the family of gamma and chi-square distributions that play major roles in the development of statistical techniques. An appreciation of how these probability models function will allow you to analyze your data with confidence that your results are reliable, solid, and correct.
|
ADVERTISEMENT |
The gamma family of distributions
Gamma distributions are widely used in all areas of statistics, and are found in most statistical software. Since software facilitates our use of the gamma models, the following formulas are given here only in the interest of clarity of notation. Gamma distributions depend upon two parameters, denoted here by alpha and beta. The probability density function for the gamma family has the form:
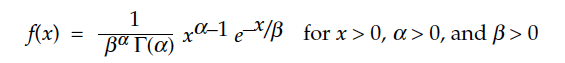
where the symbol Γ(α) denotes the gamma function (for α > 0):
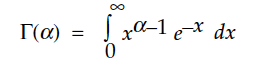
…

Comments
Typical Dr. Wheeler Article
This article is typical of Dr. Wheeler's monthly nuggets of wisdom: there are enough technical details to satisfy the brainiest of math nerds and statisticians, and enough simple explanation for the rest of us to benefit from it as well.
Dr. Wheeler is truly a national treasure.
I second that
Allow me to second your comment. Dr. Wheeler and this entire journal are true gems.
Add new comment