Photo by Carlos Andres Gomez on Unsplash
Over the past two months we’ve considered the properties of lognormal and gamma probability models. Both of these families contain the normal distribution as a limit. To complete our survey of widely used probability models, this column will look at Weibull distributions, a family that doesn’t contain the normal. As before, an appreciation of the properties of Weibull distributions will allow you to obtain results that are reliable, solid, and correct while avoiding the pitfalls of overly complex analyses.
|
ADVERTISEMENT |
The Weibull distributions
Weibull distributions are widely used in reliability theory and generally found in most statistical software packages. This makes these distributions easy to use without having to work with complicated equations. The following equations are included here in the interest of clarity of notation. The Weibull distributions depend upon two parameters, denoted here by alpha and beta. The cumulative distribution function for the Weibull family has the form:
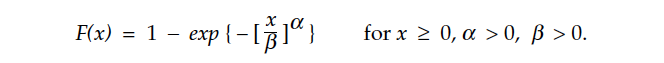
The mean of a Weibull distribution is
…

Comments
Wonderful
Another brilliant article from Dr Wheeler. Hopefully it will filter some of the noise on this topic, from the ignorant hack who has been abusing Dr Wheeler on LinkedIn.
Add new comment