Photo by Naser Tamimi on Unsplash.
When presented with a collection of data from operations or production, many will start their analysis by computing descriptive statistics and fitting a probability model to the data. But before you do this, there’s an easy test that you need to perform.
|
ADVERTISEMENT |
This test will quantify the chances that you can successfully fit any probability model to your data. By using this simple test to examine the assumptions behind all probability models, you can avoid making serious mistakes. This column will illustrate this test and explain why it works.
Example 1
The data in Figure 1 are 200 sequential values obtained over time from a single process. The average is 12.86, and the standard deviation statistic is s = 3.462. The histogram is shown in Figure 2.
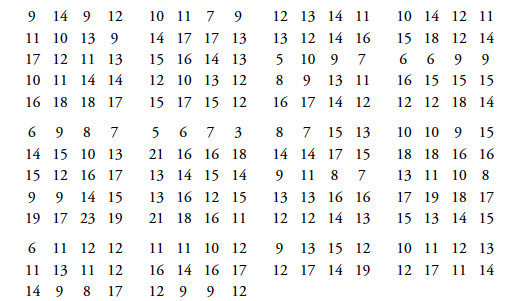
Figure 1: Example 1 data
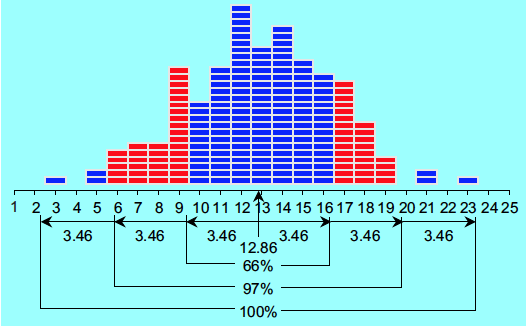
Figure 2: Histogram of the 200 values of Example 1
…

Comments
Errata
You mention Figure 9 twice but mean figure 8 the first time!
Great article. I like to be able to have constructive discussions with colleagues forcing over complicated stats on ppl. And this wil help…. ;-).
Thanks for pointing out the…
Thanks for pointing out the error. That has been fixed.
Tie Breaker
I appreciate discovering basically a test where H0 might be that "the process is statistically stable."
I also practice and teach never to compute capability until after observing a "process behavior" chart, because special cause can distort the data to "impersonate" a distribution.
But this test now allows me to handle times when the eyes and brain can't quite nail down a conclusion - when the special cause looks moderate.
Thank you!
Fantastic
Love it! It's not a test I could see that you would ever bother to use but it gives even more credence to the power of Process Behavior Charts. Very cool.
I assume this is the source? Quantitative Techniques to Evaluate Process Stability, June 2006, Quality Engineering 18(1):53-68
Add new comment