For many hundreds of years, “If it ain’t broke, don’t fix it” has summarized the predominant approach to process operation. From the physician’s admonition to do no harm, to the slightly more positive aphorism that the squeaky wheel gets the grease, there is a common theme of differentiating between those things that need to be attended to and those that don’t. When your process is in trouble, then you should do something about it. But when your process is operating OK, then leave it alone.

In production, the most common definition of trouble is “too much nonconforming product.” The common picture that comes to mind is that of Figure 1. Here, the process average is satisfactory, but the variation about the average is the problem. With these specifications, you’ll have to reduce the process variation to reduce the amount of nonconforming product.

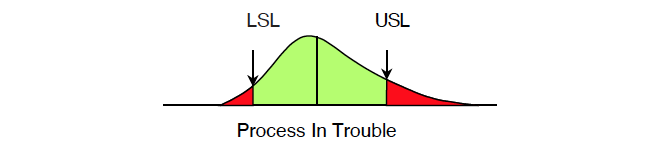
Figure 1: Traditional concept of trouble

The smooth curve of Figure 1 suggests that the variation in the process outcomes can be described by some probability model. Now, any statistician will tell you that a probability model is a description of a “sequence of independent and identically distributed random variables.” What this means in practice is that the variation can be thought of as the result of a uniform set of chance causes where no one cause has a dominant effect. This concept of a process model is part of the way scientists and engineers think. It’s the way mathematicians package variation so it can be manipulated, studied, and used.

Since the 18th century, this conceptual model for variation has proven to be a very satisfactory way to understand all sorts of variable physical phenomena. Once we have our model, we can use it to describe the phenomenon of interest at any point in time, as shown in Figure 2.

Figure 2: Traditional model for variation

The success of this model-based approach to variation in the natural sciences has made it so widespread that it has become axiomatic. It’s part of the presuppositions that we unconsciously adopt when we begin to analyze our data. As an example of this point, consider how your software presents a histogram of your data. No matter how ragged the histogram, there will usually be a smooth curve like that of Figure 1 superimposed over your data.

A change in concept

About 100 years ago, Dr. Walter Shewhart, a physicist working in industry, discovered that production processes rarely behave like natural processes. Their pattern of variation can change from day to day, and even within a day. And these changes undermine the model-based approach described above.

Figure 3: Variation in production

Here the “model” changes over time so that the collection of outcomes follows no one model. This lack of consistency from day to day makes it impossible to say with any certainty what will be produced tomorrow, much less next week or next month. Here, the process has multiple personality disorder, and the variation in outcomes is a collection of different patterns of variation.

Now, clearly no one would deliberately operate their process in the unpredictable manner shown in Figure 3. Yet the fact that most processes are operated unpredictably forces us to conclude that unpredictable operation is something that happens without notice. And this is exactly the case. Unpredictable operation is the result of the overlooked, forgotten, and ignored factors that aren’t controlled (i.e., not held constant) in practice.

While most of these factors will only have a small effect upon the process, and will therefore tend to cancel each other out, some uncontrolled factors may have effects that dominate the sum of all the other effects. When these factors, known as assignable causes, change, they tend to take the whole process along for the ride. So while the operators may not have changed a thing, the process suddenly has a different personality.

Why does this matter?

Shewhart’s insight provides an alternate approach to process improvement. When Figure 1 correctly describes your problem, you’ll have only two options: Either attempt to sort out the nonconforming product by inspection or reengineer the process to reduce the variation. Inspection will always be expensive and imperfect, and changing the process in some major way will usually be very expensive.

But when Figure 3 correctly describes your process, you can reduce the variation in the product stream by finding and controlling those assignable causes that are shifting your process around. By learning to operate your current process predictably, you can usually eliminate the nonconforming product entirely.

Figure 4: Current process operated predictably

This approach is both more effective than inspection and cheaper than either inspection or reengineering. Here, both quality and productivity increase, lowering your unit cost and improving your competitive position.

Shewhart’s insight effectively created a new definition of trouble: Your process is in trouble when it’s not operating like Figure 2. When it’s changing over time, it’s subject to assignable causes that have dominant effects upon the process outcomes, and it will be worthwhile to identify and control these assignable causes. When we combine this with the traditional definition of trouble, we end up with four possibilities.

Figure 5: The four possibilities for any process

The starting point for thinking about your process should always be the bottom row rather than the top row of Figure 5. No matter how carefully you may try to control your process, assignable causes will tend to cause it to shift around. Until you use a process behavior chart to identify these assignable causes and then control them, your process will inhabit the bottom row of Figure 5. It’s only as you identify and control assignable causes that your process will begin to behave like the pictures in the top row of Figure 5.

An inevitable consequence of controlling assignable causes will be a dramatic reduction in the process variation. Histograms become one-half, one-third, or one-fourth as wide as before. So, even when you start out in the “State of Chaos,” nonconforming product will often disappear as you operate your process more predictably, placing you in the “Ideal State.”

If you are on the “Brink of Chaos” you may think you’re operating OK, but the random walk created by the assignable causes can take you over to the State of Chaos at any time. Learning how to operate this process predictably will remove this danger and result in a process that is in the Ideal State.

(One CEO I worked with realized that by operating in the Ideal State he could go to his customer and ask for tighter specifications. When the customer agreed, the CEO had just raised the barrier on his competition.)

When you have a predictable process operating in the “Threshold State,” your process will be operating with minimum variance and some nonconforming product. To eliminate the nonconforming product, you will have to reengineer the process or change the specifications. With evidence that your process is indeed operating with minimum variation, you’ll at least have some leverage to use in negotiating relaxed specifications.

The effect of entropy

All processes belong to one of these four states. But processes don’t always remain in one state. It’s possible for a process to move from one state to another. In fact, there’s a universal force acting on every process that will cause it to move in a certain direction. That force is entropy. It continually acts upon all processes to cause deterioration and decay, wear and tear, breakdowns, and failures.

Entropy is relentless. Every process will naturally and inevitably migrate toward the State of Chaos. The only way this migration can be overcome is by continually repairing the effects of entropy. Of course, this means that the effects for a given process must be known before they can be repaired. With such knowledge, the repairs are generally fairly easy to make.

On the other hand, it’s very difficult to repair something when you’re unaware of it. But if the effects of entropy are not repaired, they’ll come to dominate the process and force it inexorably toward the State of Chaos.

Figure 6: The obstacles

The cycle of despair

Since everybody knows that they’re in trouble when their processes are in the State of Chaos, they inevitably appoint chaos managers whose job is to drag the process up from the State of Chaos. With luck, these chaos managers can get the process back to the Brink of Chaos—a state which is erroneously considered to be “out of trouble.”

Once the process is brought back to the Brink of Chaos, the chaos manager is sent off to work on another problem. But as soon as his or her back is turned, the process begins to move down the entropy slide toward the State of Chaos.

New technologies, process upgrades, and all the other “magic bullets” which may be tried can never overcome this cycle of despair. You may change technologies, but the benign neglect that inevitably occurs when the process is on the Brink of Chaos will allow entropy to drag the process back down to the State of Chaos. Thus, focusing solely upon conformance to specifications will condemn you to forever cycle between the State of Chaos and the Brink of Chaos.

The only way out

There’s only one way out of this cycle of despair. There’s only one way to move a process up to the Threshold State or the Ideal State, and that is the effective use of process behavior charts.

Every manufacturer is confronted with a dual problem—to identify both the effects of entropy and the presence of assignable causes. Entropy places a process in the cycle of despair. Assignable causes doom it to stay there.

The only way a manufacturer can ever meet the dual objectives of overcoming the barrier created by the assignable causes and counteracting the effects of entropy is by using process behavior charts. No other approach will consistently and reliably provide the necessary information in a clear and understandable form.

Summary

How you think of your data will frame your approach to data analysis. If you conceive of your data using a probability model as in Figure 7, you’re assuming your process exists as a well-defined entity.

Figure 7: The model-based approach to variation

However, a process will exist as a well-defined entity only when it’s operated predictably. And the only evidence of predictable operation comes from a process behavior chart. So, until such a chart is available, the use of Figure 7 is erroneous and misleading. The model-based approach used with natural processes doesn’t work with production processes. That’s why there are no models in SPC.

Figure 7 is not a natural state for a production process. Rather, it’s an achievement. With production data, the probable reality is more like Figure 8.

Figure 8: The starting point for thinking about process data

If we start with the conceptualization in Figure 8, then we can use process behavior charts to work toward the ideal pictured in Figure 7. But if we start with Figure 7, then we’ll have already assumed away the opportunities for improvement afforded by the use of process behavior charts.

Any process operated without the benefit of process behavior charts is ultimately doomed to operate in the State of Chaos.

The best that chaos managers can hope to achieve is to get their process to operate at the Brink of Chaos for at least a short period of time.

Process behavior charts are the only way to break out of the cycle of despair.

Donald Wheeler’s complete “Understanding SPC” seminar may be streamed for free. For details, see spcpress.com; for an example, see his column last month in Quality Digest.