Phase Two Charts and Their Probability Limits

Do you know what really happens in phase two?

Published: Monday, November 4, 2019 - 12:03

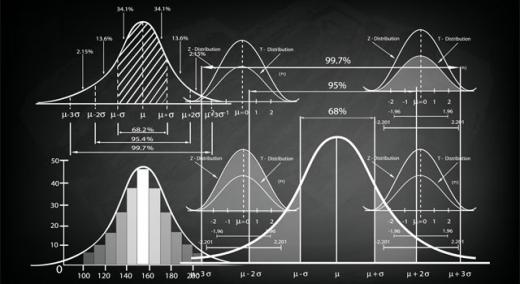
In the past two months we have looked at how three-sigma limits work with skewed data. This column finds the power functions for the probability limits of phase two charts with skewed probability models, and compares the trade-offs made by three-sigma limits with the trade-offs made by the probability limits.

Phase two charts

Ever since 1935, there have been two approaches to finding limits for process behavior charts. There is Walter Shewhart’s approach using fixed-width limits, and there is Egon Pearson’s fixed-coverage approach based on probability models. (For more on these two schools of thought, see “The Normality Myth,” Quality Digest, Sept. 19, 2019.) About the year 2000, some of my fellow statisticians tried to reconcile these two approaches by talking about “phase one and phase two control charts.”

Phase one charts use Shewhart’s fixed-width, three-sigma limits. These charts are used to help identify assignable causes of exceptional variation so that the process can be adjusted or fixed as needed. Then, under the assumption that once a process is fixed it will stay fixed, it is time for phase two.

In phase two the idea is to “fill in the details that Shewhart skipped over” by computing fixed-coverage limits. To compute these phase two, fixed-coverage limits we have to begin by selecting a probability model to represent the predictable process. Next, the parameters for this probability model are estimated from the data. Finally, this “fitted model” for the “predictable process” is used to compute limits for the phase two chart. Since these fixed-coverage limits will depend upon P = the amount of routine variation that is to be filtered out, they are known as probability limits.

So, how do you choose P? The common choice for P is 0.9973 because this is the value of P that is associated with the three-sigma limits for a normal probability model. Figure 1 shows these 0.9973 probability limits for six different probability models.

Power functions

The probability limits in figure 1 all have a false-alarm probability of [1–P] = 0.0027. But with upper limits ranging from 3.0 to 8.5 standard deviations above the mean, we have to wonder about the ability of these limits to detect signals of a process change. To characterize the sensitivity of these probability limits, we will need to find the power functions. As we did last month, let us restrict our attention to charts for individual values using detection rule one—a point falling outside the limits.

Figure 1: 0.9973 Probability limits for six probability models

To represent a process shift, we will consider the process average moving to the right by some amount, where this amount is expressed as a multiple of the standard deviation of the original model.

Figure 2: A shift in location increases the area beyond the limit.

Let the symbol a represent the probability that a value will fall above the upper probability limit after the shift in location. Also let k denote the number of observations collected following the shift. For a given shift, the probability of detecting that shift within k observations is given by the formula:

This simple formula defines the power functions for our limits, and these power functions are commonly summarized using the average run length (ARL) value for a given shift. For detection rule one, these ARL values are the inverse of the value for a.

When we carry out the operations above using the six different probability models and looking at shifts ranging from 2σ to 6σ, we get the ARL values in figure 3.

Figure 3: ARL values for 0.9973 probability limits for six different models

Now that we have summarized the power of the probability limits we can compare the characteristics of probability limits with those of three-sigma limits. The ARL values for the three-sigma limits may be found in last month’s column, “The Ability to Detect Signals,” Quality Digest, Oct. 7, 2019. In addition, the nominal alpha levels for three-sigma limits may be found in “The Normality Myth” cited earlier. We will specifically look at how both probability limits and three-sigma limits detect a 3σ shift in location. The needed ARL values and nominal alpha levels for three-sigma limits are given in figure 4.

Figure 4: Characteristics of three-sigma 3imits with skewed probability models

The normal probability model

When all that you have is an estimate of location and an estimate of dispersion, a normal distribution is your only choice for a probability model. This is because a normal model is the distribution of maximum entropy. It represents a worst-case model since the middle 90 percent of the normal distribution is spread out more than the middle 90 percent of any other model. This means that before you can ever choose any model other than a normal, you will always have to have additional information beyond an estimate of location and an estimate of dispersion.

With a normal probability model, the three-sigma limits are also the 0.9973 probability limits. For the standard normal distribution shown, these limits are ±3.00. These limits will have a nominal false-alarm probability of 0.0027, and they will detect a 3σ shift in location within 2.0 observations on the average (ARL = 2.0).

Figure 5: A normal probability model

Whenever a point falls outside these limits we know that one of two things has occurred: Either we have detected a shift in the process, or we have had a false alarm. If we interpret the point as a shift that is 3σ or greater, then we expect that this shift occurred on the average within the past 2.0 points since the ARL for a 3σ shift is 2.0. If we are wrong, and no shift occurred, then over the past ARL = 2.0 points we have incurred an average risk of a false alarm of:

Average False Alarm Probability = 1 – [ 1 – nominal alpha ]^ARL = 0.0054

So, with a normal probability model, when a point falls outside the limits, either we have observed a shift large enough to be interesting, or we have observed a rare event that occurs about five times per thousand. By using both the ARL for a 3σ shift and its corresponding average false-alarm probability, we can characterize how the two different approaches to computing limits will work as signal detection techniques with the different models.

A Weibull probability model

The Weibull distribution with a shape parameter of 1.6 and a scale parameter of 1.00 has a mean of 0.8966 and a standard deviation of 0.5737. This model has a boundary value of zero that is 1.56 standard deviations below the mean.

Figure 6: A Weibull probability model

The upper three-sigma limit is 2.62, and the boundary value of zero replaces the lower three-sigma limit. From figure 4, these limits have a nominal alpha level of 0.0094 and an ARL of 2.3 for a 3σ shift. This ARL has an average false-alarm probability of:

Average False Alarm Probability = 1 – [ 1 – 0.0094 ]^2.3 = 0.0215

The upper probability limit of 3.255 is 4.11 sigma above the mean. The lower probability limit of 0.013 is 1.54 sigma below the mean. These limits have a nominal alpha level of 0.0027. From figure 3 these limits have an ARL of 3.3 for a 3σ shift, and this ARL has an average false-alarm probability of:

Average False Alarm Probability = 1 – [ 1 – 0.0027 ]^3.3 = 0.0089

With this Weibull model the probability limits have an average false-alarm probability of 0.9 percent vs. 2.1 percent for the three-sigma limits; however, the penalty for using the probability limits is that they will take about 50-percent longer to detect a 3σ shift in location.

A chi-square model with eight degrees of freedom

The chi-square distribution with eight degrees of freedom (d.f.) has a mean of 8.0 and a standard deviation of 4.0. This model has a boundary value of zero that is two standard deviations below the mean.

Figure 7: The chi-square probability model with eight d.f.

The upper three-sigma limit is 20.0 and the boundary value of zero replaces the lower three-sigma limit. From figure 4, these limits have a nominal alpha level of 0.0103 and an ARL of 2.3 for a 3σ shift. This ARL has an average false-alarm probability of:

Average False Alarm Probability = 1 – [ 1 – 0.0103 ]^2.3 = 0.0235

The upper probability limit of 25.36 is 4.34 sigma above the mean. The lower probability limit of 0.92 is 1.77 sigma below the mean. These limits have a nominal alpha level of 0.0027. From figure 3 these limits have an ARL of 3.9 for a 3σ shift, and this ARL has an average false-alarm probability of:

Average False Alarm Probability = 1 – [ 1 – 0.0027 ]^3.9 = 0.0105

With this chi-square model, the probability limits have an average false-alarm probability of 1.1 percent vs. 2.4 percent for the three-sigma limits; however, the penalty for using the probability limits is that they will take about 70-percent longer to detect a 3σ shift in location.

A chi-sqaure model with four degrees of freedom

The chi-square distribution with four d.f. has a mean of 4.0 and a standard deviation of 2.828. This model has a boundary value of zero that is 1.41 standard deviations below the mean.

Figure 8: The chi-square probability model with four d.f.

The upper three-sigma limit is 12.5 and the boundary value of zero replaces the lower three-sigma limit. From Figure 4, these limits have a nominal alpha level of 0.0141 and an ARL of 2.5 for a 3σ shift. This ARL has an average false-alarm probability of:

Average False Alarm Probability = 1 – [ 1 – 0.0141 ]^2.5 = 0.0349

The upper probability limit of 17.8 is 4.88 sigma above the mean. The lower probability limit of 0.10 is 1.38 sigma below the mean. These limits have a nominal alpha level of 0.0027. From figure 3 this chart has an ARL of 4.5 for a 3σ shift, and this ARL has an average false-alarm probability of:

Average False Alarm Probability = 1 – [ 1 – 0.0027 ]^4.5 = 0.0121

With this chi-square model the probability limits have an average false-alarm probability of 1.2 percent vs. 3.5 percent for the three-sigma limits; however, the penalty for using the probability limits is that they will take about 80% longer to detect a 3σ shift in location.

An exponential model

The exponential distribution used here has a mean of 2.0 and a standard deviation of 2.0. This model has a boundary value of zero that is one standard deviation below the mean.

Figure 9: An exponential probability model

The upper three-sigma limit is 8.0, and the boundary value of zero replaces the lower three-sigma limit. From figure 4, these limits have a nominal alpha level of 0.0183 and an ARL of 2.7 for a 3σ shift. This ARL has an average false-alarm probability of:

Average False Alarm Probability = 1 – [ 1 – 0.0183 ]^2.7 = 0.0486

The upper probability limit of 13.22 is 5.61 sigma above the mean. The lower probability limit of 0.004 is 0.998 sigma below the mean. These limits have a nominal alpha level of 0.0027. From figure 3 this chart has an ARL of 5.2 for a 3σ shift, and this ARL has an average false-alarm probability of:

Average False Alarm Probability = 1 – [ 1 – 0.0027 ]^5.2 = 0.0140

With an exponential model the probability limits have an average false-alarm probability of 1.4 percent vs. 4.9 percent for the three-sigma limits; however, the penalty for using the probability limits is that they will take almost twice as long to detect a 3σ shift in location.

A lognormal model

The lognormal distribution with a location parameter of 1.00 and a shape parameter of 1.00 has a mean of 1.649 and a standard deviation of 2.161. This model has a boundary value of zero that is only 0.76 standard deviations below the mean.

Figure 10: A lognormal probability model

The upper three-sigma limit is 8.13, and the boundary value of zero replaces the lower three-sigma limit. From figure 4, these limits have a nominal alpha level of 0.0180 and an ARL of 3.2 for a 3σ shift. This ARL has an average false-alarm probability of:

 Average False Alarm Probability = 1 – [ 1 – 0.0180 ]^3.2 = 0.0565

The upper probability limit of 20.09 is 8.53 sigma above the mean. The lower probability limit of 0.065 is 0.733 sigma below the mean. These limits have a nominal alpha level of 0.0027. From Figure 3 this chart has an ARL of 12.5 for a 3σ shift, and this ARL has an average false-alarm probability of:

Average False Alarm Probability = 1 – [ 1 – 0.0027 ]^12.5 = 0.0332

With this lognormal model the probability limits have an average false-alarm probability of 3.3 percent vs. 5.6 percent for the three-sigma limits; however, the penalty for using the probability limits is that they will take four times as long to detect a 3σ shift in location.

The trade-offs

Every decision procedure has to make a trade-off between the ability to detect a signal and the risk of a false alarm. The table in figure 11 summarizes the trade-offs found above for each of the six models by listing the ARL and the corresponding average false-alarm probability (AFA) for each model and both sets of limits.

Figure 11: ARL values and average false-alarm probabilities for 3σ shifts

These values are plotted in figure 12 using the ARL values for a 3σ shift in location on the vertical scale and the corresponding average false alarm probabilities on the horizontal scale. Since, for a normal model, the three-sigma limits are the same as the probability limits, the normal model belongs to both curves. The remaining points on each curve correspond to the five skewed models in the order shown in figure 11.

Figure 12: The trade-offs made by the two approaches

Figure 12 makes clear the different philosophies inherent in each approach. The probability limits of phase two charts have a primary objective of avoiding false alarms even at the expense of decreasing sensitivity. The three-sigma limits of phase one charts have a primary objective of detecting process changes in a timely manner, while maintaining a reasonable risk of a false alarm.

When interpreting figure 12 it is instructive to remember that virtually every statistics class teaches that a false-alarm probability of 5 percent is acceptable. Only in the last case do the three-sigma limits have an average false alarm probability that slightly exceeds this traditional risk.

Average run lengths for false alarms

The average false-alarm probabilities above characterize the risk that we take when we interpret a point outside the limits as a signal of a process change. They are the risk associated with a specific interpretation.

But these average false alarm probabilities are not the same as the overall risk of a false alarm. To characterize this overall risk, we use the average run length between false alarms (ARL₀). This is simply the average run length for the power function when there is no signal present. For detection rule one with a chart for individual values, this ARL₀ value is the inverse of the nominal false-alarm probability for the limits. The nominal alpha values for the probability limits in figure 1 are all 0.0027. The nominal alpha values for the three-sigma limits are listed in figure 4. When we invert these nominal alpha values, we get the ARL₀ values in figure 13.

Figure 13: Average run lengths between false alarms

These average run lengths between false alarms provide a guide for what happens when your processes are steady and unchanging. When your process remains unchanged for hundreds of successive points, the probability limits will yield an average of one false alarm per 370 points.

When your process remains unchanged for hundreds of successive points, and when it is modeled by one of the skewed models, three-sigma limits will yield an average of one false alarm per 100 points, one per 71 points, or one per 55 points, depending upon the model used. (When was the last time your process behavior chart had 50, 70, or 100 successive values without any points going outside the limits?)

But there is more to the decision process than avoiding false alarms. To understand the values above, we need to consider how predictable processes operate.

A very predictable process

In “How Do You Get the Most Out of Any Process?” Quality Digest, Nov. 7, 2016, I tell the story of one of the most predictable processes I have seen in 40 years of consulting. This process was actively monitored on a continuing basis, and signals of process changes were attended to in a timely manner. By attending to these signals they not only maintained their process in a reasonably predictable state, but they also reduced the process variation by one-third.

They collected and measured one part at each of four times each day, and combined these four values into one subgroup per day. In 380 days of operation, they detected seven signals of a change in location on their average chart. Each of these were investigated, assignable causes were found, and corrective actions were taken. The seventh process change was detected on day 324, which gives an average run length between process changes of 324/7 = 46 subgroups.

If this process, which had been operated predictably for years, only averaged 46 subgroups between upsets, how realistic is it to assume that your process is going to remain unchanged for hundreds of points in succession?

In this world, regardless of how carefully a process is operated, upsets will affect that process. When you have one or more real process changes every 20, 30, or 40 subgroups, it hardly matters whether your ARL₀ value is 55, 71, 100, or 370. When the average run length between process changes is less than the average run length between false alarms, then the most likely explanation for any point that falls outside the limits will still be a process change.

Using probability limits in order to boost the ARL₀ value from 55, 71, or 100 up to 370 is simply buying insurance that you do not need.

Summary

Phase one charts, with their three-sigma limits, look for evidence of changes in the process so that we can take action to improve the process for the future. By discovering the dominant cause-and-effect relationships that affect your process, and by making these causes part of the set of controlled inputs to your process, you gain leverage to operate on target while reducing the process variation. And operating on target with minimum variance will do more to reduce the excess costs of both production and use than anything else you can do.

This is why those who want to learn how to operate their processes up to their full potential will always prefer phase one charts.

Phase two charts, with their probability limits, seek to minimize the occurrence of false alarms at the expense of detecting process changes in a timely manner. They make an implicit assumption that once a process has been fixed, it will stay fixed. Unfortunately, this assumption is simply not true. Your process is always going to be subject to upsets. The only question is how long will it take for you to find out about these upsets?

This is why those who do not want to rock the boat will prefer phase two charts with their unquestioned lack of sensitivity.

So, let’s say that you have gotten your process to the point that it displays a reasonable degree of predictability. Can you sharpen up the limits by using a phase two chart? No, you will never get probability limits to be more sensitive than three-sigma limits. Regardless of the probability model you choose, and regardless of the P value you use, probability limits always turn out to be less sensitive than three-sigma limits. And that is why you never need to worry about phase two charts. They represent a complex, academic strategy that is always suboptimal. Phase one charts are all you will ever need.

In practice the ability to react to process changes is more important than protecting yourself from occasional false alarms. And three-sigma limits preserve this ability even when the process, when operated predictably, produces a skewed histogram.

So do not worry so much about straining out the gnats of false alarms that you end up swallowing the camels of undetected process changes.

About The Author

Donald J. Wheeler

Find out about Dr. Wheeler’s virtual seminars for 2023 at www.spcpress.com. Dr. Wheeler is a fellow of both the American Statistical Association and the American Society for Quality who has taught more than 1,000 seminars in 17 countries on six continents. He welcomes your questions; you can contact him at djwheeler@spcpress.com.