"Skew-whiff" Credit: Bahi
The shape parameters for a probability model are called skewness and kurtosis. While skewness at least sounds like something we might understand, kurtosis simply sounds like jargon. Here we’ll use some examples to visualize just what happens to a probability model as kurtosis increases. Then we’ll combine the visible effects of both skewness and kurtosis to see how they combine to “shape” probability models
|
ADVERTISEMENT |
Last month, we found that while an increase in positive skewness measures a nearly invisible increase in the area of the upper tail, it has two visible manifestations. Specifically, these are a substantially shorter lower tail and an appreciable shift of the mode to the left. Figure 1 summarizes these results for the three comparisons made.
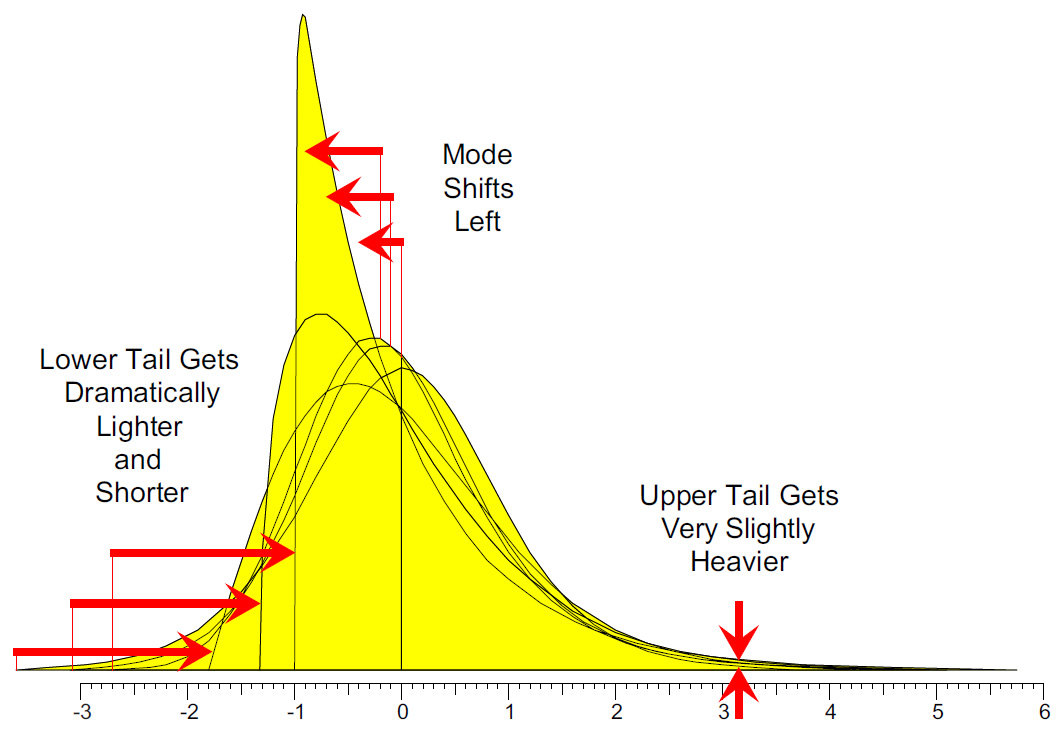
Figure 1: Effects of increasing positive skewness while holding kurtosis constant
Figure 1 shows what happens when we hold the kurtosis constant and increase the skewness. In the comparisons that follow, we’ll look at what happens when we increase the kurtosis while holding the skewness constant.
…

Comments
Excellent
I love how Dr. Wheeler explains the mathematical details for those who care about such things, but boils it all down to what 99.9% of all practitioners need to know in a just few key sentences using simple language at the end.
Dr. Wheeler is a treasure as he is one of the few who tries to simplify things instead of complicate them unnecessarily.
Add new comment