These days, my memory isn’t what it used to be. Besides that, my memory isn’t what it used to be. But my incurable case of CRS (can’t remember stuff) is not nearly as bad as that of the exponential distribution.

When modeling failure data for reliability analysis, the exponential distribution is completely memoryless. It retains no record of the previous failure of an item. That might sound like a bad thing. But this special characteristic makes the distribution extremely useful for modeling the behavior of items that have a constant failure rate.

Using the exponential distribution to model failure data

Suppose you track the time until failure of a randomly collected sample of items. When you graph the results on a histogram, you get something like this:

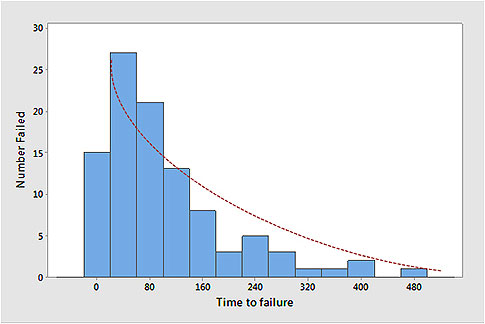
Notice that the number of items that fail at a given point in time decreases steadily as time elapses. This steady decrease can be fit nicely to an exponential curve.

 …