Eighty-four doctors treated 2,973 patients, and an undesirable incident occurred in 13 of the treatments (11 doctors with one incident and one doctor with two incidents), a rate of 0.437 percent. A p-chart analysis of means (ANOM) for these data is shown in figure 1.

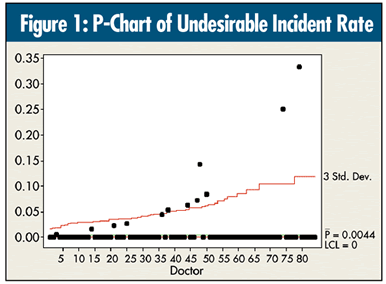
This analysis is dubious. A good rule of thumb: Multiplying the overall average rate by the number of cases for an individual should yield the possibility of at least five cases. Each doctor would need 1,000 cases to even begin to come close to this!

The table in figure 2 uses the technique discussed in last month’s column, “A Handy Technique to Have in Your Back Pocket,” calculating both “uncorrected” and “corrected” chi-square. Similar to the philosophy of ANOM, I take each doctor’s performance out of the aggregate and compare it to those remaining to see whether they are statistically different. For example, in figure 2, during the first doctor’s performance, one patient in the 199 patient treatments had the incident occur. So, I compared his rate of 1/199 to the remaining 12/2,774.

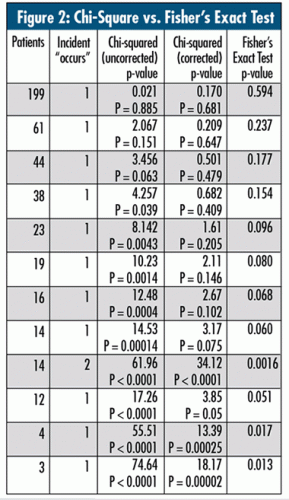
Things break down very quickly as the denominator size decreases, especially the gap between the “uncorrected” and “corrected” chi-square values.

 …