Invisible Probability Models

The gap between computations and reality

Published: Monday, June 4, 2018 - 11:03

Some properties of a probability model are hard to describe in practical terms. The explanation for this rests upon the fact that most probability models will have both visible and invisible portions. Understanding how to work with these two portions can help you to avoid becoming a victim of those who, unknowingly and unintentionally, are selling statistical snake oil.

Visible and invisible distributions

When a continuous probability model has an infinite tail or tails, that probability model can be divided into a visible portion and an invisible portion. To illustrate this I will use the probability density function for a standardized Burr distribution shown in figure 1.

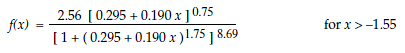
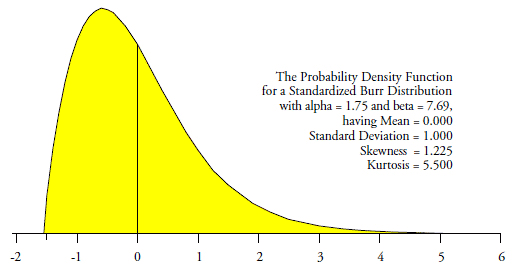
Figure 1: A standardized burr distribution

No matter what vertical scale we adopt when drawing this probability density function, at some point the curve will merge with the axis and we will have reached the end of the visible portion of this probability model. In figure 1 the height of the curve will have dropped to less than 1/300th of the maximum height by the time we get out to a point that is five standard deviations above the mean. The remainder of this probability model, from x = 5 to x = infinity, will constitute the invisible portion of the distribution.

This happens with every probability model having an infinite tail or tails. When we draw the distribution as a whole, even though the tails may go out to infinity, it is impossible to draw the portions out beyond four or five standard deviations on either side of the mean. At any practical scale we may choose, the last one or two parts per thousand in an infinite tail will end up being invisible.

So let us define the invisible portion of a probability model as the most extreme part per thousand in each infinite tail. For the standard normal distribution this definition results in a visible portion that ranges from –3.09 to 3.09 and which contains 0.998 of the total area. This is why accurate representations of a normal distribution result in a visual portion that falls within 3.1 standard deviations on either side of the mean.

Figure 2: A standard normal distribution

Thus, probability models with infinite tails can be divided into visible and invisible portions. This distinction becomes important when we use probability models in practice to calculate probabilities and make predictions. Before we can discuss the implications of working with the visible and invisible portions of a probability model, we will need to first discuss what is involved in making predictions.

Making predictions

All data are historical. All analyses of data are historical. Yet all the questions of interest pertain to the future. So how can we use our historical data to make predictions?

When presented with a collection of numbers we can always compute descriptive summaries such as the average and the standard deviation statistic. We can even organize the numbers and draw our histograms and our running records. When the context makes it logical to compute these numerical and graphic summaries, the question becomes, “How can we use these statistics to make predictions?” And the answer is that we can extrapolate from our data to make predictions only when the data display a reasonable degree of homogeneity.

Nonhomogeneous data

If the data do not display a reasonable degree of homogeneity, then we know that the process that produced those data was changing in the past. If these changes were unexpected and unexplained, then we are likely to continue to have unexpected and unexplained changes in the future. So while our nonhomogeneous historical data may describe the past, they will not provide a basis for making predictions.

When our data do not display a reasonable degree of homogeneity we have to think of the data as coming from multiple sources. But a probability model is defined to be a limiting characteristic for an infinite sequence of observations from a single phenomenon. When we find evidence that our data are not homogeneous, it becomes irrational to attempt to use a single probability model to approximate a collection of data that represent different phenomena. Hence, regardless of the rationalizations used, when we know our data are not homogeneous, any attempt to “fit” a probability model to the histogram is patent nonsense.

Homogeneous data

If the data have displayed a reasonable degree of homogeneity in the past, then the process producing those data is likely to continue to produce similar data in the future and the process may be said to be predictable. Here the historical data may be used as the basis for making reasonable predictions. So the primary question of data analysis is always the question of homogeneity.

Now the only reliable way to determine if a data set is homogeneous is to organize those data in a rational manner and put them on a process behavior chart. If the data appear to be reasonably homogeneous, then the computations for the process behavior chart will also provide the basis for several useful predictions regarding the process average, the process dispersion, the fraction nonconforming, and the natural process limits. In most cases these predictions based on the process behavior chart will be sufficient in practice.

Using probability models

Once we have evidence that our process is being operated in a reasonably predictable manner, the introduction of a probability model is not required, but it is no longer completely inappropriate. Here the probability model we select will essentially provide an approximation for our histogram, and as such it might be used to make predictions about our predictable process. However, when doing this we must be careful to respect the limitations of using a probability model as an approximation for our histogram.

All histograms have finite tails. When we use a probability model to approximate a histogram we can only work with the finite amount of data given. Consequently, it will always be the visible portion of the probability model that provides the approximation to our histogram.

Now the invisible portion of a probability model is a function of the visible portion. Specifically, it is an artifact of the mathematical curve used to approximate the histogram in the visible portion. In spite of this relationship between the visible and invisible portions, the invisible portion of the probability model that you have selected does not actually characterize any aspect of your data, neither does it tell you anything about the underlying process.

“But wait, can we not verify that we have the right model, thus making the invisible portion appropriate?” No, we cannot. Lack-of-fit tests may eliminate some models as being unrealistic, but they can never verify a particular model as being the “right” model. This is what makes the invisible portion of a probability model arbitrary.

While mathematical variables may run off and join the infinity circus, real data never do. At some point there will always be a parting of the ways between your probability model and your histogram. This divorce may occur before you get to the invisible portion, but it will certainly occur once you get into the invisible portion of your selected distribution.

Thus, when working with any probability model, you should always regard the last part per thousand in an infinite tail as highly suspect. While it will always be an artifact of the selected model, it is unlikely to be a characteristic of your process. As a consequence, those computations that are substantially affected by the invisible portion of a distribution should also be treated as suspect. They are unlikely to be useful in making realistic predictions about your process. To illustrate this we first consider predicting the fraction of nonconforming product.

Data-based prediction of the fraction nonconforming

When we have a process that has been operated predictably in the past the data will be homogeneous, and we can use these historical data to make a prediction regarding the conformity of future production. Say we have 200 observations in our homogeneous data set, and that all 200 values fall within the specification limits. Then our number examined will be n = 200, our observed number nonconforming will be Y = 0, and our point estimate of the fraction nonconforming will be zero.

However, due to the nature of data, there will always be some uncertainty attached to this estimate. To characterize this uncertainty we will use a 95-percent Agresti-Coull interval estimate for the fraction nonconforming. The central value for this interval estimate is defined to be:

And the 95-percent Agresti-Coull interval estimate is found using:

So, while our observed fraction nonconforming is zero, the uncertainty in this value results in a prediction of “something less than 2.3 percent nonconforming.” To get a tighter data-based prediction we will need a larger number of homogeneous data.

Model-based predictions of the fraction nonconforming

Now let us assume that a normal probability model is used with the 200 data from above to make a prediction regarding the fraction nonconforming. Further let us assume that the specifications fall at 3.8 standard deviations on either side of the average. Then, based on the tables of the normal distribution, we would predict 144 parts per million nonconforming for our process. Notice how much more precise and exact this is than the “something less than 2.3 percent” found earlier.

However, if we had reason to fit the Burr distribution from figure 1 to the 200 data above, with specifications falling at ±3.8 standard deviations from the average, then we would predict 4,320 parts per million nonconforming for our process. This is 30 times larger than the previous prediction of 144 ppm! Clearly, our model-based prediction will depend upon which model we select. Nevertheless, we still have a number that is so much more precise and exact than the data-based prediction.

But how much uncertainty should be attached to these model-based predictions? As soon as we ask this question we run into a fact of life: The uncertainty for the model-based predictions cannot be less than the uncertainty for the data-based prediction. We cannot reduce our uncertainty by fitting an assumed model to our data—the uncertainty of the assumption can only add to the uncertainty inherent in the data. We simply cannot leverage our 200 data into supporting parts-per-million computations by fitting some probability model to those data.

So, using a normal probability model, our prediction is 144 parts per million with an interval estimate of zero to 23,325 parts per million!

Using the Burr model of figure 1 our prediction is 4,320 parts per million with an interval estimate of zero to 23,325 parts per million!

Using our data-based prediction our estimate is zero, with an interval estimate of zero to 2.3 percent nonconforming.

Given the uncertainty of zero to 2.3 percent, the three point estimates of zero, 144 ppm, and 4,320 ppm are simply three estimates of the same thing!

Figure 3: Estimating the fraction nonconforming

As long as we are working with the homogeneous data set of 200 values, our interval estimate of the fraction nonconforming will remain “something less than 2.3 percent nonconforming.” And this will remain true regardless of how many mathematical gyrations we may use in obtaining our point estimate. While the probability models allow us to compute numbers that seem more precise and exact than what we get from our data-based prediction, all this supposed precision and exactness is nothing more than smoke and mirrors that serve to distract the statistically naive.

For more on this problem see my column “Estimating the Fraction Nonconforming” (Quality Digest, June 2011).

Computing probabilities in practice

Whenever we use a distribution to compute a probability we may think we are working in the parts per million range, but the results are seldom good to more than parts per thousand. Regardless of the number of decimal places we use, a probability model fitted to a few dozen or a few hundred homogeneous data cannot really be expected to give results that are better than three decimal places.

It might seem that by using more data we could refine our probability model and get probabilities that would be good to more than three decimal places, but there is a problem with this approach. As we increase the size of our data set we also increase the chances that the data will not be homogeneous. When the data become nonhomogeneous the fitted model breaks down and the computed probabilities become less precise rather than more precise.

Finally, probability models can never be good to parts per million simply because the last part per thousand will always be in the invisible portion of the model. Since the invisible portion of a probability model does not actually characterize any aspect of the data, working with increments smaller than 0.001 will result in numbers that are more characteristic of the model selected than they are of the underlying process (e.g., 144 ppm vs. 4,320 ppm). The invisible portion of the probability model simply does not tell us anything about the underlying process.

And that is why, when analyzing data, probability models are rarely useful for computations beyond parts per thousand.

Does this mean that all parts per million values are nonsense? No, we still have the data-based approach which does not make any assumptions about the data beyond requiring them to be reasonably homogeneous. I have clients that have failure rates down in the dozens of parts per million. These data-based values are computed based on millions of data each day. While these are true observed rates, each of these values is merely a description of a particular day. Before these values can be used to make predictions about what will happen tomorrow we will need to know if a sequence of such historical values displays a reasonable degree of predictability.

Process parameters

“Yes, but can we not use the probability models to gain insight into the process parameters?” To examine this idea we shall consider to what extent the mean, variance, skewness, and kurtosis parameters depend upon the invisible portion of a probability model.

The mean

For a continuous probability model, f(x), the mean value is defined by the area between the x-axis and a curve. This curve is called the product curve. It consists of the set of points that result when we multiply x by f(x) for all values of x. This area between the product curve and the horizontal axis is shaded in figure 4. The visible portion of this Burr distribution extends from –1.55 to +5.0, and the invisible portion extends from 5.0 to infinity.

Figure 4: Computing the mean value for the Burr distribution in figure 1

To discover the relationship between the visible portion of the distribution and the mean value we will ignore the negative sign for the area below the axis and simply add up all of the areas between the product curve and the axis. Here we get 0.388 + 0.384 + 0.004 = 0.776. Of this total area, 0.772 comes from the visible portion of this distribution, and 0.004 comes from the invisible portion. Hence, the visible portion of this distribution accounts for 0.772/0.776 = 0.995 or 99.5 percent of the mean value parameter, and the most extreme part-per-thousand of this probability model (the invisible portion) accounts for one-half percent of the area used to determine the mean value. Thus, the mean value is primarily dependent upon the visible portion of this distribution.

The variance

When a probability model, f(x), has a mean value of zero we may define the variance of that model as the area between the x-axis and the product curve obtained by multiplying x-squared and f(x). For the Burr distribution given in figure 1 this area between the product curve and the horizontal axis is shaded in figure 5.

Figure 5: Computing the variance for the Burr distribution in figure 1

The sum of the areas between the product curve and the axis is 1.000, which is the variance for this probability model. Here we find that 97 percent of the total area comes from the visible portion of the distribution and 3 percent comes from the invisible portion. Thus, the variance is primarily dependent upon the visible portion of this distribution.

The skewness

When a probability model, f(x), has a mean value of zero and a variance of one, the skewness of that model may be generically defined by the area between the x-axis and the product curve obtained by multiplying x-cubed and f(x). This area is shaded in figure 6 (for the visible portion of the Burr distribution).

Figure 6: Computing the skewness for the Burr distribution in figure 1

The skewness for this distribution is 1.587 – 0.362 = 1.225. The total area used in computing the skewness is 1.949, and 1.747 of this total comes from the visible portion of this probability model. Thus, 89.6 percent of the skewness comes from the visible portion of this distribution, and the last part per thousand of the distribution (the invisible portion) contributes 10.4 percent of the area used to define the skewness parameter!

The kurtosis

When a probability model, f(x), has a mean value of zero and a variance of one, the kurtosis of that model may be generically defined as the area between the x-axis and the product curve obtained by multiplying x-to-the-fourth-power and f(x). This area is shaded in figure 7 (for the visible portion of the Burr distribution).

Figure 7: Computing the kurtosis for the Burr distribution in figure 1

The kurtosis for this distribution is 5.500. Of the area used to compute this value only 4.214 or 76.6 percent came from the visible portion of this distribution. The last part per thousand of this distribution (the invisible portion) contributed 23.4 percent of the area used to determine the kurtosis parameter!

Other probability models

To generalize the results above I looked at the parameters for the 73 standardized Burr distributions represented by the dark dots in figure 8. (The probability models are shown for 18 of these 73 distributions to help the reader to understand the wide range of shapes included in this set.)

Figure 8: 73 Burr distributions on the shape characterization plane

For each of these 73 models I computed the contributions of the visible portion to the computation of the mean, the variance, the skewness, and the kurtosis parameters. The table in figure 9 summarizes these results for each parameter. For each set of 73 percentages, figure 9 gives the minimum, average, and maximum contributions attributable to the visible portion of the distributions.

Figure 9: Percentages of parameter computations attributable to visible portion of distribution

Across this set of 73 probability models we find that about 99 percent of the mean value, and about 95 percent of the variance, comes from the visible portion of the distribution. These two parameters are highly dependent upon the visible portion of the model, which is why they provide effective summaries for the visible portion of any distribution.

For these 73 distributions the visible portion contributes between 76 percent and 97 percent of the skewness parameter, and between 43 percent and 95 percent of the kurtosis parameter. Thus, the invisible portion contributes up to 24 percent of the skewness and up to 57 percent of the kurtosis here. The fact that such large percentages of the areas used to compute these parameters depend upon the last part per thousand of the distribution is what makes it virtually impossible to describe, in English or any other language, what skewness and kurtosis actually “measure.”

Additionally, when we understand the extent to which the parameters for skewness and kurtosis depend upon the last part per thousand of the model, we can begin to understand why the statistics for skewness and kurtosis are essentially useless. Until we have a homogeneous data set containing tens of thousands of observations the skewness and kurtosis statistics will simply be incomplete. This is why you should continue to ignore the skewness and kurtosis statistics provided by your software. They have absolutely no practical utility.

The lesson of figure 9 is that virtually all of the useful information that can be extracted from our data by means of descriptive numerical summaries will be contained in measures of location and measures of dispersion.

Summary

Once we understand the impact of the invisible distribution upon our computations we can begin to understand the limitations of those computations in practice. Because the invisible portion of a distribution inhabits the mathematical plane, we can and do use it to perform computations. However, as these computations become more dependent upon the invisible portion they become increasingly arbitrary because of the divorce between the invisible portion and the underlying realities.

When we compute a tail-area probability it can be used out to three decimal places at most. If we interpret a tail area beyond three decimal places we will be leaving our data behind and interpreting differences that are not supported by the data. When we compute values smaller than 0.001 we are playing in the realm of the invisible distribution where our computations are no longer constrained by any aspect of reality.

This has serious implications for those who convert capability indexes into fractions nonconforming, for those who attempt to compute false alarm probabilities, and for those who attempt to define probability-based limits for process behavior charts. While these computations may work reasonably well when you are dealing with the visible portion of a probability model, they loose all credibility when they are based solely upon the invisible portion.

So while your software may compute infinitesimal areas under the extreme tails of a probability model, you should not be so gullible as to believe that these model-based parts per million values have any contact with reality.

All data are historical. All statistics are historical. All the questions of interest pertain to the future. To determine if we can use our historical data to make predictions, we need to examine a sequence of such data to see if they are reasonably homogeneous or not. And the primary technique for this is a process behavior chart. When making predictions based on a homogeneous data set, virtually all of the practical predictions of interest can be made using the information from the process behavior chart, without reference to any probability model.

About The Author

Donald J. Wheeler

Dr. Wheeler is a fellow of both the American Statistical Association and the American Society for Quality who has taught more than 1,000 seminars in 17 countries on six continents. He welcomes your questions; you can contact him at djwheeler@spcpress.com.