It’s usually not a good idea to rely solely on a single statistic to draw conclusions about your process. Do that, and you could fall into the clutches of the “duck-rabbit” illusion shown below.

If you fix your eyes solely on the duck, you’ll miss the rabbit—and vice-versa.

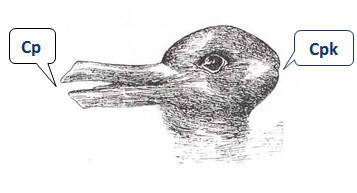
If you’re using Minitab Statistical Software for capability analysis, the capability indices Cp and Cpk are good examples of this. If you focus on only one measure, and ignore the other, you might miss seeing something critical about the performance of your process. 

Cp: A tale of two tails

Cp is a ratio of the specification spread to the process spread. The process spread is often defined as the 6-sigma spread of the process (that is, 6 times the within-subgroup standard deviation). Higher Cp values indicate a more capable process.

When the specification spread is considerably greater than the process spread, Cp is high.

 …