Credit: Richard Carter
Last month I mentioned that we can put autocorrelated data on a process behavior chart. But what is autocorrelated data and what does it tell us about our processes? This article will use examples to answer both of these questions.
Autocorrelation (aka serial correlation) describes how the values in a time series are correlated with other values from that same time series. The most interesting form of autocorrelation is the lag 1 autocorrelation, which describes how successive values are correlated with each other. This article will focus exclusively on lag 1 autocorrelation.
For our first example we will use the residual viscosities from a distillation column. The first 10 values, in units of stokes, are 473, 450, 464, 459, 450, 462, 481, 456, 451, and 447. The average is 459.3 and the average moving range is 12.89. The XmR chart for these data is shown in figure 1. These 10 values are reasonably homogeneous and contain no apparent signals of a change in the operation of the distillation column.
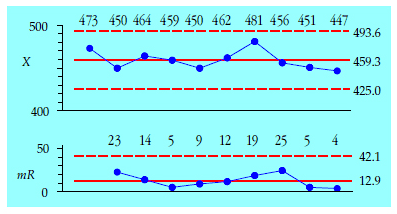
Figure 1: XmR chart for residual viscosities for periods 1 to 10
Since autocorrelation is concerned with pairs of points we begin by using these 10 successive values to define nine pairs of points:
…

Add new comment