Last month I looked at how the fixed-width limits of a process behavior chart filter out virtually all of the routine variation regardless of the shape of the histogram. In this column I will look at how effectively these fixed-width limits detect signals of economic importance when skewed probability models are used to compute the power function.
|
ADVERTISEMENT |
Power functions
A power function provides a mathematical model for the ability of a statistical procedure to detect signals. Here we shall use power functions to define the theoretical probabilities that an X chart will detect different sized shifts in the process average. To compute a power function we begin with a probability model to use, and a shift in location for that model. Figure 1 shows these elements for a traditional standard normal probability model.
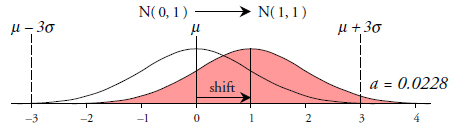 Figure 1: Normal model with a 1.0-sigma shift in location |
…

Comments
The Ability to Detect Signals
As always, I enjoy reading Dr. Wheeler's articles in Quality Digest. In this instance, the article started off well for me, then veered off in a direction with which I'm uncomfortable. Initially the article addresses a one sigma shift in data representing a normal distribution. But in commenting on Figure 2, Dr. Wheeler begins to focus on a three sigma shift and maintains this focus throughout the rest of the article. Indeed, under a subheading "The Results", he says, "Process behavior charts are intended to detect those process changes that are large enough to be of economic interest. In most cases these will be shifts in location in the neighborhood of three sigma or greater."
I am retired after 40 years in manufacturing and no longer have access to much real world data, but my impression is that most shifts are less than three sigma and would therefore take more data to detect with a process behavior chart than is suggested here.
Bill Pound
Bill, thanks for the kind words. I used one sigma shifts in the figure because of the issue with the scales for larger shifts. In my experience when processes shift around, they commonly shift by two-sigma or more. However, if you are interested in smaller shifts the skewed models are more sensitive than the normal model.
Add new comment