Statistical Tolerance Intervals

How to make exact predictions

Published: Monday, January 4, 2016 - 16:35

One computation that modern software offers to unsuspecting users is the statistical tolerance interval. Since this sounds very much like limits for individual values, some have been tempted to use them on process behavior charts in place of the traditional three-sigma limits for individual values. To discover what tolerance intervals do, and do not do, read on.

Confidence intervals and tolerance intervals

Last month we considered the theoretical and practical aspects of finding a confidence interval for the mean. On the theoretical plane this involved finding the formula for a random interval that would bracket the mean value with some specified probability. In figure 1 this probability which is shown as 90% is the value commonly known as the "confidence level" for the interval estimate.

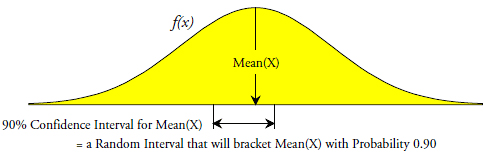
Figure 1: A 90% confidence interval for the mean

Instead of computing an interval estimate for a parameter such as the mean or variance of a probability model, we might wish to compute an interval estimate for the region that will encompass some proportion, P, of the area under the probability model. If we let the values A and B define the shortest interval with coverage P for the designated probability model, then the problem becomes one of how to estimate the interval defined by A and B. To this end we find a formula for a random interval that will bracket the interval [A, B ] with some probability which we refer to as the confidence level. Thus, a tolerance interval not only has a confidence level, it also has a coverage value P. Since both of these values are less than 1.00 it is important to distinguish the confidence level from the coverage value when discussing tolerance intervals. The common convention is to state the confidence level first and the coverage last. A 90% tolerance interval with coverage P is shown in figure 2.

Figure 2: A 90% tolerance interval with coverage P

Most books on statistics do not include tolerance intervals. First, it is a confusing topic for beginning students. Second, it requires very complex computations involving numerical integrations. What follows is based on a book of tables by Robert E. Odeh and Donald B. Owen published in 1980. While the underlying mathematics has not changed, software packages that compute tolerance intervals may use various shortcuts, approximations, or formulas that have been developed since Odeh, Owens, and others worked out the mathematical foundations.

The general formula for a 100[1 – alpha]% tolerance interval for proportion P is:

Average ± k [ Standard Deviation Statistic ]

where k depends upon the confidence level, [1 – alpha], the proportion covered, P, and the number of data used, N. Some normal theory values for k from Odeh and Owen may be found in figure 3.

As the coverage value P gets larger the interval [A, B] will get wider. Also, as the confidence level goes up the increased ambiguity needed to achieve the greater confidence level will force the tolerance interval to get wider. For this reason a tolerance interval with a large confidence level and a large P value will be very wide indeed. For example, the interval [A, B] that defines the middle 99 percent of a normal distribution is:

MEAN(X) ± 2.576 SD(X)

while for N = 10, the normal theory 99%/99% tolerance interval is:

Average ± 5.610 Standard Deviation Statistic

By comparing the 5.610 with the 2.576 we find that this tolerance interval is 118 percent wider than the interval being estimated. To obtain less inflated estimates of the tolerance you will need to make some compromise between confidence and coverage when attempting to use tolerance intervals. The usual compromise is to use a smaller confidence level. Here a 95%/99% tolerance interval for N = 10 would be:

Average ± 4.437 Standard Deviation Statistic

which is only 72 percent wider than the interval [A, B] that is being estimated.

So, what is the purpose of a tolerance interval? Since we do not need an elaborate computation to summarize the past values, the only logical purpose for a tolerance interval must be the prediction of future outcomes for some production process. The coverage value P is the percentage of the future process outcomes to be captured by the prediction, and the confidence level, [1–alpha], is the proportion of the time we hope to capture that percentage P.

Figure 3: Normal theory k values for tolerance intervals for proportions P

The table in figure 3 contains the three commonly used confidence levels of 99%, 95% and 90% plus the factors for 50% confidence levels. The three larger confidence levels allow you to compute an interval that has a high likelihood of actually bracketing the middle proportion P. These intervals estimate the tolerance limits plus their uncertainties. The 50% confidence level factors allow you to actually estimate the tolerance limits. Thus, a 50%/99% tolerance interval actually allows you to estimate the points A and B that correspond to the middle 99 percent of a normal distribution having the mean and variance of your process. (This can be seen in the way the factors for the 50% confidence level intervals approach the standard normal values of 1.645, 1.960, 2.576. and 2.807 as N gets large.)

"But what happens if a normal distribution is not an appropriate model for our process?"

Non-normal data

While the values in figure 3 were developed using a normal probability model, the values in three of the four columns for P are sufficiently general to be used with non-normal data. As shown in my September 2012 and October 2012 columns, the middle 90 percent of a normal distribution is as wide or wider than the middle 90 percent of any other distribution. As a result, the normal theory values in figure 3 for P = 0.90 may be used with any probability model as a worst case tolerance interval for P = 0.90. For example, based on 50 data, a normal theory 95%/90% tolerance interval is given by the interval:

Average ± 1.999[ Standard Deviation Statistic ]

When this interval is used with 50 data from any other probability model it will have a confidence level of at least 95 percent that it will cover at least 90 percent of a homogeneous product stream. For this reason, the columns in figure 3 for P = 0.90 may be used to produce completely universal, worst-case, distribution-free, tolerance intervals.

As shown in my columns for August, September, and October of 2015, the middle 95 percent of a normal distribution is approximately the same as the middle 95 percent of most other probability models. Thus, the normal theory values in figure 3 for P = 0.95 may be used to obtain approximate tolerance intervals for P = 0.95 that will work for virtually any probability model. For example, based on 50 data, a normal theory 95%/95% tolerance interval is given by the interval:

Average ± 2.382[ Standard Deviation Statistic ]

When this interval is used with 50 data from any other probability model it will have a confidence level of approximately 95 percent that it will cover at least 95 percent of a homogeneous product stream. Thus, the columns in figure 3 for P = 0.95 are essentially distribution-free.

It is only with the more extreme values for P that the values in figure 3 become specific to a normal distribution. However, since virtually all unimodal probability models will have at least 98 percent of their area within three standard deviations of the mean, we can use the last column of normal theory values (for P = 0.995) to obtain approximate tolerance intervals for P = 0.98 for non-normal probability models. For example, based on 50 data, a normal theory 95%/99.5% tolerance interval is given by the interval:

Average ± 3.409[ Standard Deviation Statistic ]

When this interval is used with 50 data from any other probability model it will have a confidence level of approximately 95 percent that it will cover approximately 98 percent or more of a homogeneous product stream. Thus, the columns in figure 3 for P = 0.995 can be adapted to obtain approximate distribution-free tolerance intervals for P = 0.98. So while the values in figure 3 were developed using a normal probability model, most can be used to get approximate tolerance intervals that will work for virtually all unimodal probability models.

How tolerance intervals work

Two examples will be used to illustrate how tolerance intervals work in practice. The first uses the Line Three data of figure 9. Using all 200 values we find an average of 10.10 and a global standard deviation statistic of 1.79. Using these values an estimate for the middle 99 percent of the product stream is provided by the 50%/99% tolerance interval of 5.47 to 14.73.

To illustrate how tolerance intervals work in practice the Line Three data were subdivided into sets of N = 10 values each and a 95%/99% tolerance interval was found for each subset. The histogram of the 200 data and the twenty tolerance intervals are shown in figure 4.

We would expect approximately 19 out of the 20 tolerance intervals in figure 4 to bracket at least 99 percent of the product stream. Here all 20 intervals do so. However, by insisting that approximately 95 percent of the intervals will bracket a least 99 percent of the product stream we end up with intervals with end points ranging from -1 to 21 when the middle 99 percent of this process is found between 6 and 14. Thus, our "predictions" regarding the product stream are over twice as wide as the actual product stream.

Figure 4: Twenty 95%/99% tolerance intervals for line three

Our second example will use the data from Line Seven shown in figure 10. Using all 200 values we find an average of 12.86 and a global standard deviation statistic of 3.46. Using these values an estimate for the middle 99 percent of the product stream is provided by the 50%/99% tolerance interval of 3.91 to 21.81.

As before, to see how tolerance intervals work in practice, these 200 data were subdivided into sets of N = 10 values each and a 95%/99% tolerance interval was found for each subset. The histogram and the 20 tolerance intervals are shown in figure 5.

Figure 5: Twenty 95%/99% tolerance intervals for line seven

Here, like the proverbial blind squirrel, three of our 95%/99% tolerance intervals (intervals 8, 10, and 20) actually managed to bracket at least 99 percent of the 200 values from Line Seven! The other 17 tolerance intervals came up short, and this happened in spite of the fact that these intervals were inflated over 72 percent relative to the target interval. So, rather than getting intervals that cover at least 99 percent of the data 95 percent of the time, we get intervals that perform as expected only 15 percent of the time!

On the other hand, the region actually covered by 19 out of the 20 tolerance intervals (using all but interval number 9) is the region shaded in white. This region includes observed values of 11 to 17 and contains 64 percent of these 200 data. So either our 95%/99% tolerance intervals ended up covering 64 percent of the product stream 95 percent of the time; or else they covered 99 percent of the product stream 15 percent of the time! Either way, one of our excessively precise confidence and coverage values fails miserably.

Of course, as we learned last month, the problem with Line Seven is that it was being operated unpredictably. The formulas for the tolerance intervals, like everything else in statistical inference, explicitly assume that we are working with independent and identically distributed random variables. When the data are not homogeneous this assumption is inappropriate and the inferences break down. The formulas may be used to compute numbers, but the numbers will no longer mean what you expect them to mean. Once the foundation assumption is removed the whole inferential structure will collapse.

So, the first problem with tolerance intervals is that they will only work when you are characterizing the product stream for a process that is being operated predictably. And the only way to operate a process predictably is to use a process behavior chart to establish and maintain predictable operation. Thus, the only time that statistical tolerance intervals function as advertised is when they are used in conjunction with a process behavior chart. So how do they differ from the computations used with a process behavior chart?

Three sigma limits

The limits on a process behavior chart are commonly known as three-sigma limits. Mathematically, these limits are essentially a 50%/99.7% tolerance interval (computed using a within-subgroup measure of dispersion rather than a global one). This shift in the confidence level and the different basis for the computation make a world of difference. The three-sigma limits of a process behavior chart are intended to filter out the probable noise in order to help the user identify potential signals of process changes. They separate the routine variation from the exceptional variation. To do this they estimate the values for A and B rather than trying to bracket A and B.

When exceptional variation is present we know that there is a dominant assignable cause that is affecting our process. When we can identify that assignable cause we can then either compensate for it or make it part of the set of control factors for our process. Either way we remove its effects from our product stream, which increases product consistency and lowers our scrap and rework rates. With increased consistency and reduced scrap and rework costs we can deliver higher quality at lower cost, which is the way to take over markets. Thus, three-sigma limits tell us when to take action on the process.

If we fail to act when we should we will have missed an opportunity to identify a dominant cause-and-effect relationship that affects our process outcomes. When we fail to identify a dominant cause-and-effect relationship we will continue to suffer the consequences of having an unpredictable process. As the unknown, yet dominant, assignable cause varies over time it will take our process on walkabout. When our process goes on walkabout we will suffer increased variation in the product stream, and possibly increased scrap and rework costs. With lower product quality and increased costs we can only become increasingly non-competitive.

Thus, our objective in computing limits for our process behavior charts is to filter out virtually all of the routine variation, but no more. If our limits are too wide we will miss signals and will fail to take action when it is needed. If they are too narrow we will have too many false alarms. Shewhart found that three sigma limits provide the right balance between the economic consequences of these two mistakes. Thus, the ultimate justification for the use of three-sigma limits does not come from any mathematical argument, but is economic in nature. We have decades of empirical evidence that three sigma limits work. They have been proven to do a very good job of separating the probable noise from those signals that are of economic consequence in all kinds of processes and with all kinds of data.

Tolerance intervals vs. process behavior charts

"So, can we use tolerance intervals in place of three-sigma limits?" Consider what happens with our two example data sets.

Line Three: For the 200 values of Line Three the average is 10.10, the global standard deviation statistic is s = 1.79, and the 95%/99.5% tolerance interval is:

Average ± 3.069 Standard Deviation Statistic = 10.10 ± 3.069(1.79) = 4.6 to 15.6

If we place the 200 values for Line Three on an XmR chart we will find our average value to be 10.10 and our average moving range to be 1.955. To convert this average range into a within subgroup measure of dispersion, Sigma(X), we divide by d2 = 1.128 to get 1.73. Thus, our three-sigma natural process limits for individual values are:

Average ± 3 Sigma(X) = 10.10 ± 3 (1.73) = 4.9 to 15.3

Thus, the three-sigma limits for individual values and the 95%/99.5% tolerance interval tell the same story for Line Three. Virtually all of the routine variation will be found between 5 and 15 (which agrees with the histogram in figure 4). These two computations converge because this process is being operated predictably and there are no signals of exceptional variation here.

Line Seven: For the 200 values of Line Seven the average is 12.86, the global standard deviation statistic is s = 3.46, and the 95%/99.5% tolerance interval is:

Average ± 3.069 Standard Deviation Statistic = 10.10 ± 3.069 (3.46) = 2.2 to 23.5

None of the 200 values fall outside this interval.

Figure 6: Line seven: Using a 95%/99.5% tolerance interval as limits

When we place the 200 values from Line Seven on an XmR chart we find our average value to be 12.86 and our average moving range to be 2.281. To convert this average range into a within subgroup measure of dispersion, Sigma(X), we divide by d2 = 1.128 to get 2.02. Thus, our natural process limits for individual values are:

Average ± 3 sigma(X) = 12.86 ± 3 (2.02) = 6.8 to 18.9

Fifteen of the 200 values fall outside these three-sigma limits as may be seen in figure 7. These fifteen points are all potential signals of exceptional variation. They tell us that these data are not homogeneous and that the process is going on walkabout. With the process going on walkabout you cannot have any confidence that the tolerance interval of 2.2 to 23.5 will characterize future process outcomes.

Figure 7: The X chart for line seven:

It is important to note that it is not the multipliers of 3 and 3.069 that create the difference between the natural process limits and the tolerance interval, but rather it is the difference between the global measure of dispersion (which implicitly assumes homogeneity) and the within-subgroup Sigma(X) measure of dispersion (which is skeptical about the assumption of homogeneity). This difference goes back to the secret foundation of statistical inference, and is fundamental. This is why you cannot turn a tolerance interval into a reasonable technique for filtering out the noise by simply fine-tuning your choice of confidence and coverage levels.

Summary

Tolerance intervals assume the data are homogeneous, while process behavior charts actually examine the data for evidence of a lack of homogeneity.

Tolerance intervals use a global measure of dispersion, while process behavior charts use a within-subgroup measure of dispersion.

Tolerance intervals try to embrace almost all of the data, while process behavior charts seek to separate the routine variation from the exceptional variation within the data.

Tolerance intervals seek to estimate properties of the product stream without determining if the product stream exists is a well-defined entity. Process behavior charts tell us when to take action on the process with the objective of getting it to operate as a well-defined entity.

Thus, tolerance intervals have a different purpose than the three sigma limits of a process behavior chart. Any attempt to use tolerance intervals as a substitute for three sigma limits for individual values reveals a fundamental lack of understanding of these profound differences between the two techniques.

While the confidence levels and coverages of tolerance intervals offer the unsuspecting user enticing exactness, the reality is somewhat different. First there is the issue of having to specify a probability model. Since we will never have enough data to ever verify any particular probability model, the assumption of a probability model becomes the first approximation involved with using a tolerance interval. When we combine this approximation with the approximation that occurs as we move from the theoretical plane to the data analysis plane, we find that in practice the apparent exactness of a tolerance interval is more of an illusion than a reality.

But the greater problem is the use of a global measure of dispersion with a tolerance interval. If the data are actually homogeneous, a global measure of dispersion is appropriate and will help the tolerance interval actually bracket the desired proportion, P. However, if the data are not homogenous the interval computed will have no fixed relationship with the desired proportion P. When this happens the apparent exactness expressed by the confidence level and the coverage value P is nothing more than make-believe. Both the confidence level and the coverage value become fairy tales for credulous adults.

While tolerance intervals will predict future process outcomes for a predictable process, they do not work as advertised with unpredictable processes. And the only way to know if a tolerance interval is appropriate is to demonstrate, by means of a process behavior chart, that the process has been operated predictably over a reasonable period of time.

So we end up in a catch-22 situation. The only time that a tolerance interval will work as advertised is when it will be approximating exactly the same thing that is already characterized by the natural process limits of the process behavior chart. When the tolerance interval gives you something different, it is the tolerance interval that is flawed, not the natural process limits.

Figure 8: Interpreting X chart three sigma limits as a 95%/100P% tolerance interval

Finally, if your boss should want the enticing exactness of a tolerance interval, use the values from figure 8 to interpret your natural process limits. As noted earlier, the natural process limits of an XmR chart are logically equivalent to a 50%/99.7% tolerance interval. However, when using an XmR chart with limits based upon the average of [k–1] two point moving ranges, you may interpret the natural process limits as a 95% tolerance interval for at least 100P percent of a homogeneous product stream. So, say that your XmR chart shows that you have a predictable process, and your baseline contains k = 30 values, then your natural process limits are effectively a 95%/97% tolerance interval for your product stream.

Of course, if your process is not being operated predictably, all predictions are futile. (What part of unpredictable do you not understand?) The natural process limits will approximate what your process can achieve when operated predictably, but your reality is going to be something much worse until you take action to find and control the unknown assignable causes that make your process behave unpredictably.

Figure 9: Line three data and twenty 95%/99% tolerance intervals

Figure 10: Line seven data and twenty 95% / 99% tolerance intervals

About The Author

Donald J. Wheeler

Find out about Dr. Wheeler’s virtual seminars for 2023 at www.spcpress.com. Dr. Wheeler is a fellow of both the American Statistical Association and the American Society for Quality who has taught more than 1,000 seminars in 17 countries on six continents. He welcomes your questions; you can contact him at djwheeler@spcpress.com.