Problems With Process Capability Calculations

Calculating Cpk for runout (and other GD&T specifications)

Thu, 11/21/2013 - 12:23

A few days ago we received an email from a friend at a machine shop. He had just finished a process capability analysis for a critical feature (a runout on a cylindrical part) and was shocked by the output. The spreadsheet software he used showed him a process capability (Cpk) of 0.39 (see figure 1 below).

ADVERTISEMENT

To put this in perspective, with a Cpk of 0.39, he should be seeing a nonconformance rate of between 12 percent and 24 percent, assuming a stable process and a normal distribution. However, he was actually experiencing a nonconformance rate close to zero. In fact, he hadn’t had any problems with runout as far back as he could remember.


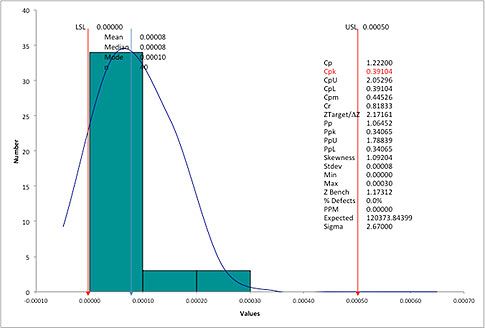
Figure 1: Runout histogram. Click here for larger image.

 …

Want to continue?
Log in or create a FREE account.
By logging in you agree to receive communication from Quality Digest. Privacy Policy.

Comments

In this example, there is no LSL, just an upper specification limit (USL).In the QI Macros, if you specify the USL with no LSL, Cpk=Cpu would be 2.05 instead of 0.39.

We could substitute median for the average to get 1.91, but in either case Cpk is much greater than 1.66 (5 sigma) and close to 2.0 (6 sigma).

Yes, in this case a median will be a better measure of central tendency, but do we really need a micrometer or is this yardstick good enough? While Average could easily be changed to Median in the QI Macros Histdata worksheet, would it tell a better story?

The QI Macros do have a true position Cp Cpk template for GD&T calculations (using variation both from X and Y coordinates).

 

 

Thanks for the explanation of the features in qimacros. Sounds like a good product. Yes, in this case, the difference in calculations was not large, but given a different distribution, we could see very different results. In any case, the larger point is that the user needs to understand the “nature of the specification” and the type of distribution he or she is dealing with, and understand the relevant process capability measure (Cpu in this case). Nipun & John

Submitted by bdaniels on Thu, 11/28/2013 - 03:44

Why are we in the Quality profession still espousing this psuedo statistic?  

All these girations to calculate a single number that is simply not informative or actionable.

What does the index tell us that the run chart (multi-var or control chart) doesn't?  nothing.

We must start with it to determine stability.  We must go back to it to begin to understand how to improve the process.  We must go to it to understand if the index is even reasonably correct...

Thank you! We agree that the control chart or the multi-vari chart are the most-informative tools, and that you must begin with stability. In fact, we addressed the importance of stability in the link provided above to a previous blog (pitfalls to avoid with process capability analysis) which we hope people will take a few minutes to read. We have tried to list some of the common issues we have encountered in that blog. However, we find that machine shops and many other suppliers are required to report Cp, Cpk calculations by their customers. In many cases, there is no training provided, and incorrect interpretations are very common. Nipun & John

I couldn't agree more.  Capability indicies are one of the most abused statistics.  Management likes them because they boil everything down to one number.  I had a professor term this mononumerosis. 

For a very good discussion on capability indices, refer to the January 2002 issue of ASQ "Journal of Quality Technology."  The entire issue is dedicated to this subject.

Submitted by caseyem on Wed, 12/04/2013 - 08:31

I couldn't agree more with BDaniels. I understand the authors' reply that sometimes these are "required." Yet, when we perfunctorily make these calculations without understanding the meaning or purpose of the number, we do ourselves and others little good. Fine report the number, but then also report what is useful and meaningful and actionable. Maybe people will eventually drop the useless information requirement.

The authors identify that IF the formula requires assumptions, then common errors will often be due to violations of those assumptions.

But, the formula in itself does not require either stability or normality--nor does the meaning of the concept. These are assumptions added by people who thought they were necessary. They can be circumvented, the authors suggest one way, by understanding the meaning of process capability. The meaning--at least the one I would want to use--is the probability of meeting specification(s).

This is the meaning I give it regardless of the index. Different process capability indices differ only in the conditions under which that probability is determined. 

But since we can only estimate the probability for some of these conditions, e.g., what is the "best" the process is capable of?--then we need to understand whether adding assumptions make those estimates better, when, and how? Sometimes the assumptions are neither useful nor necessary.

Just as we should recognize when Cpk is useful/necessary or not, we should also recogize when stability and normality assumptions are useful/necessary or not.

Add new comment