Capability indexes allow us to characterize the relationship between the process potential and the specifications. Performance indexes characterize the past performance relative to the specifications. Yet, in practice, we seek to make sense of these index numbers by converting them into other quantities such as the fraction nonconforming or the parts per million (ppm) defect rates. This article will outline a better way to make sense of capability and performance indexes by converting them into the effective cost of production and use.
|
ADVERTISEMENT |
Let us define the effective cost of production and use as:
The actual cost of producing and using an item (the numerator) will consist of the nominal cost of production plus the average excess costs per unit associated with producing and using such items.
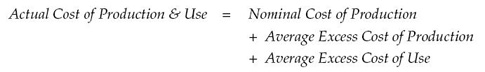
…
Comments
Convincing Management To Take Action
How does one convince an operations manager that loss is occuring and action should be taken to center the process when the Cp and Cpk are greater than 2? Especially, with no defects occurring, how do you convince the manager that loss is occurring?
Ignorance Is Bliss
Ignorance is indeed bliss. The production manager needs educating, not convincing. He/she can only convince themselves.
Add new comment