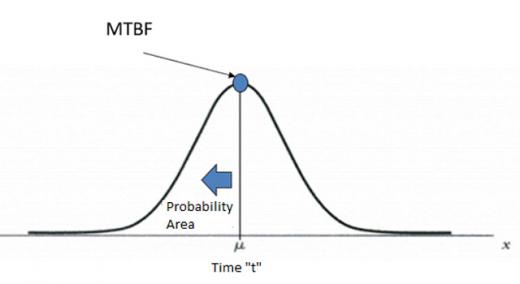
Within maintenance management, the term MTBF (mean time between failures) is the most important key performance indicator after physical availability.

Unlike MTTF (mean time to failure), which relates directly to available equipment time, MTBF also adds up the time spent inside a repair. That is, it starts its count from a certain failure and only stops when the fault is remedied, and the equipment restarted and performing again. According to ISO 12489, this indicator can only be used for repairable equipment, and MTTF is the equivalent of nonrepairable equipment.

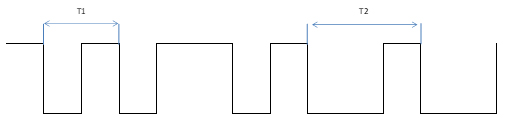
The graphic below illustrates these occurrences:

To calculate the MTBF in figure 1, we add the times T1 and T2 and divide by two. That is, the average of all times between one failure and another, as well as its return, is calculated. It is, therefore, a simple mathematical calculation. But what does MTBF mean?

 …