Inspection sounds simple. Screen out the bad stuff and ship the good stuff. However, measurement error will always create problems of misclassification where good stuff is rejected, and bad stuff gets shipped. While guard-bands and tightened inspection have been offered as a way to remedy the problem of shipping bad stuff, it turns out that they are often prohibitively expensive in practice. Here we look at how tightened inspection improves the quality of the product stream and compare those improvements with the associated excess costs.
|
ADVERTISEMENT |
The problem of inspection
A product measurement, X, may be thought of as consisting of the product value, Y, plus some measurement error, E, so that X = Y + E. With this model, the relationship between X and Y can be shown using a bivariate normal probability model where:
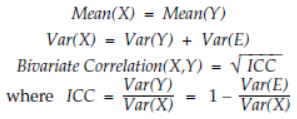
…

Add new comment