In May 2019, James Beagle and I published an article that contained tables for the analysis of mean moving ranges or ANOMmR (pronounced a-nom-m-r). By request of those using this technique, I have expanded these tables. This article contains these expanded tables and repeats the illustrative example from the earlier paper.

Say you have m measurement devices and you wish to know if these devices have equivalent amounts of measurement error. Also assume that each of these devices is used to repeatedly measure a standard item k times. When repeated measurements of a standard are placed on an XmR chart the resulting chart is known as a consistency chart. 

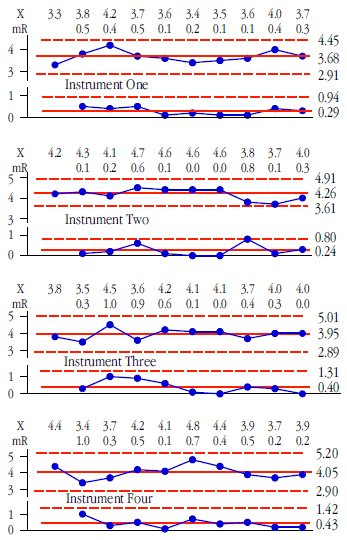
Figure 1: Consistency charts for instruments 1, 2, 3, and 4

 …