To control color, you need to be able to compare very small differences, determine their impact and understand how to address that impact. In this series we’ve already looked at the history of color analysis and the role of light in tolerancing. Here we’ll discuss the difference between a color space and a color tolerance, and introduce the most common methods.

Color spaces

A color space gives us a way to communicate color. Just like we can find any location on planet Earth using longitude, latitude, and altitude, we can locate any color in color space.

Here are the two most common color spaces:

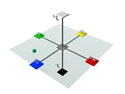L*a*b*, aka CIELab, aka LAB Model

During the 1940s, Richard Hunter introduced a tri-stimulus model, Lab, which is scaled to achieve near uniform spacing of perceived color differences.

 …