Electronic distance measurement (EDM) instruments, such as laser trackers, total stations, and handheld laser distance meters, have been used in a limited number of nondestructive testing (NDT) and structural health monitoring (SHM) applications attempting to measure bridge deflections and vibrations. However, a survey of the literature reveals that, by far, most attempts have been by measuring elevation angles with robotic total stations.
|
ADVERTISEMENT |
One case was found that used a Leica AT401 laser tracker, but it also measured deflections by measuring the elevation angle, i.e., like the total station cases, the measurement architecture did not exploit the higher accuracy and speed of EDM. One case was found using a noncommercial laser-ranging instrument, similar to handheld laser distance meters, that did measure vertical deflections of a bridge, from the instrument fixed on the ground to a point directly above the instrument, at 200 measurements/second, with good results. Only one case reported 3D measurements, using a total station. All other cases only reported vertical deflections.
Attendance at NDT/SHM conferences has revealed that most engineers in those fields are unaware of the measurement capabilities of such instruments; only one person in any of the conversations had heard of a laser tracker, and no EDM instrumentation was on the exhibit floors. The American Society for Nondestructive Testing (ASNT) produces a large number of publications, and issues NDT competence certifications, but does not include EDM instruments in any of its handbooks, training manuals, or certification requirements. A two-volume set of books on SHM, published in 2012, does not list EDM as a measurement option. The 2017 Transportation Research Board Conference (TRB) did have one paper that used a Metris MV224 Laser Radar, but it was used in a girder fabrication application. A presentation on the new Federal Highway Administration NDE facilities and instrumentation did not mention any dimensional metrology instrumentation. A recurring theme in the literature is the effort spent trying to determine if a particular total station was capable of measuring with sufficient resolution and frequency to determine bridge deflections and vibrations. Results of the literature survey are reported in detail in a paper presented at the SPIE Smart Structures NDE Conference in March 2017.
Based on the literature, it is clear that present manufacturers’ instrument specifications do not meet the needs of NDT and SHM researchers. In some cases, the specifications may be artificially limited, due to constraints introduced by assumptions as to how the instrument will be used, that may not apply to new and novel applications outside the conventional customer base. Suggestions are made as to what instrument manufacturers could relatively easily do to provide meaningful specifications, for currently available instruments, to early adopters in potentially huge blue ocean markets. Example fill-in-the-blank templates are provided as a starting point. An argument is made for the need for high-accuracy 3D measurements for NDT. In addition to bridge applications, other novel applications are suggested. For example, NDT of pressure vessels, cranes, amusement park rides, and tensioning/detensioning concrete.
Introduction
This is the second in what is to be a series of papers on the use of electronic distance measurement (EDM) instruments for nondestructive testing (NDT) and structural health monitoring (SHM). The first paper1 (First Paper) was presented at the SPIE Conference on Nondestructive Characterization and Monitoring of Advanced Materials, Aerospace, and Civil Infrastructure 2017. It was intended to be an introduction to EDM and coordinate measurement metrology for the NDT community.
This article, which is intended to be an introduction to NDT for the Coordinate Metrology Society (CMS) community, will be cumulative, so those interested in the subject should also read the First Paper, which is incorporated by reference.
First Article abstract:
By using three, or more, electronic distance measurement (EDM) instruments, such as commercially available laser trackers, in an unconventional trilateration architecture, 3D coordinates of specialized retroreflector targets attached to cardinal points on a structure can be measured with absolute uncertainty of less than one part per million. For example, 3D coordinates of a structure within a 100-m cube can be measured within a volume of a 0.1-mm cube (the thickness of a sheet of paper). Relative dynamic movements, such as vibrations at 30 Hz, are typically measured 10 times better, i.e., within a 0.01-mm cube. Measurements of such accuracy open new areas for nondestructive testing and finite-element model confirmation of stiff, large-scale structures, such as buildings, bridges, cranes, boilers, tank cars, nuclear power plant containment buildings, post-tensioned concrete, and the like by measuring the response to applied loads, changes over the life of the structure, or changes following an accident, fire, earthquake, modification, etc. The sensitivity of these measurements makes it possible to measure parameters such as linearity, hysteresis, creep, symmetry, damping coefficient, and the like.
For example, cracks exhibit a highly nonlinear response when strains are reversed from compression to tension. Due to the measurements being 3D, unexpected movements, such as transverse motion produced by an axial load, could give an indication of an anomaly—such as an asymmetric crack or materials property in a beam, delamination of concrete, or other asymmetry due to failures. Details of the specialized retroreflector are included.
Introductory paragraph:
It is the thesis of this paper that the use of electronic distance measurement for nondestructive testing and structural health monitoring has been overlooked, or misapplied, outside of the aerospace and precision manufacturing industries. Significant opportunities are available in the civil, structural, mechanical, and software engineering fields, as well as expanded markets for instrument manufacturers, dimensional metrology measurement service providers, and software companies. In order to capitalize on these opportunities, an introduction to what has heretofore been disparate fields may be helpful in expanding communications between the fields.
Selected excerpts of the First Paper will be repeated herein.
Nondestructive testing (NDT) and structural health monitoring (SHM)
In section one of the First Paper, the subsections “An introduction to Electronic Distance Measurement” and “An introduction to Large-Scale Dimensional Metrology” will probably already be somewhat familiar to the Coordinate Metrology Society (CMS) community. The second section of the First Paper, “Present Relationship Between the NDT, SHM, and EDM Communities,” will probably be less familiar and more interesting.
The NDT and SHM communities in the United States are most closely associated with conferences sponsored by the American Society for Nondestructive Testing (ASNT), the Transportation Research Board (TRB), and SPIE. The TRB falls under committees AHD30, Structures and Maintenance; AFF40, Testing and Evaluation of Transportation Structures; and AHD30(3) Structural Health Monitoring, Joint Subcommittee of AHD30, AHD35, and AFF40. The International Federation of Surveyors (FIG) Working Group 6.1, Deformation Measurement and Analysis; and The International Association of Geodesy (IAG) Sub-Commission 4.2, Applications of Geodesy 2 in Engineering, also sponsor conferences on SHM. The American Society for Nondestructive Testing (ASNT) produces a large number of publications, and issues NDT competence certifications, but does not include EDM instruments in any of its handbooks, training manuals, or certification requirements. An informal survey by the author, in conversations with the attendees at those conferences in the past year, leads one to believe that the use of laser trackers is practically nonexistent among those communities. Civil and structural engineers rarely need dimensional accuracies in the part-per-million range for construction purposes, so it is understandable that they are not familiar with the capabilities of EDM.
There was one paper by Fuchs and Chase2 at TRB 2017 that used a Metris MV224 Laser Radar to eliminate shop assembly of steel bridges by measuring the component girders and doing a virtual fit-up, based on the measured hole patterns, i.e., a steel fabrication application—not NDT. This was related to similar reports3,4 and a patent application5 by Fuchs, as well as a patent application by Pettersson6 and patents to Marsh et al.7–9 It is particularly revealing that the conventional state of the art for dimensional control of bridge girder fabrication relies on steel tapes, and curved girders are fabricated by music wire and rulers to measure the sag. Splice-plate bolt holes for girder joints are match-drilled in place, with adjacent girders actually placed and blocked in a trial erection at the fabrication shop, in order to ensure they will fit properly at the construction site. There was a lot of excitement among bridge engineers about Fuchs’ system, which measures the as-built girders and bolt holes with high accuracy, and calculates the hole locations for the splice plates in a virtual assembly, i.e., eliminating trial erection at the fabrication shop.
Ettouney and Alampalli published a two-volume set of books titled Infrastructure Health in Civil Engineering.10,11 In Volume I, under section 5.4 “Sensor Measurement in SHM,” they list the following sensors: strain sensors, position, accelerometers (angular and linear), velocity (angular and linear), displacement (angular and linear), force, inclinometers, corrosion, pressure, temperature, other, and advanced sensing technologies. There is no mention of laser trackers, total stations, or EDM.
Webb et al., did an extensive literature survey focusing on bridge SHM deployments.12 In the Introduction, they state:
“Unfortunately, many existing monitoring endeavors do not have a clearly defined objective. Instead, seemingly sensible parameters are measured without proper consideration given to how the data will be interpreted. Data interpretation is then considered at a later date, often coupled with the discovery that very little useful information can be obtained. A more rational approach to the design of SHM systems is needed.”
They go on to state:
“There are few examples where SHM systems have been reported to actually demonstrate value to the operators of the structure—there may be justifiable reasons for how the collected data may prove useful to someone in the future, but the actual benefit to the system owner is rarely evident. Instead, the primary purpose of the majority of deployments is simply demonstrating that a particular new sensor technology can measure a parameter of interest rather than specifically to provide information that will inform decision making.”
In other words, this is a potentially huge blue ocean market for someone who can provide the more rational approach and solve the metrology problems for departments of transportation, railroads, and other operators of civil structures.
They divided the SHM deployments into five categories: 1) anomaly detection; 2) sensor deployment studies; 3) model validation; 4) threshold check; and 5) damage detection.
Note that, consistent with Ettouney and Alampalli, none of the deployments in the Webb survey used EDM. At the presentation of the First Paper, only one person in the audience responded that he was familiar with laser trackers.
However, EDM has been attempted in a limited number of cases. In particular, the First Paper’s subsection, “Historic use and misuse of EDM for NDT and SHM,” illustrates the problem(s) with a case study3 of specific examples.13–29 The First Paper reviews each of the cited cases in some detail. Additional cases30–36 suffer from similar problems, but will not be reviewed in detail here.
The subsection of the First Paper summarizes the reviews of the cited cases with the following observations.
“While results obtained by these examples are mixed, they do illustrate the potential utility of augmenting the standard sensor-based instrumentation used for SHM to include EDM. There are common problems among these examples:
• The instrument manufacturers do not provide enough useful specification information for dynamic applications.
• The short-range specifications for laser trackers may be discouraging possible novel applications.
• Laser trackers should be considered vs. total stations during the initial planning stages.
• The measurement architecture and geometry should exploit the high accuracy of the distance measurements.
• An error analysis should be done before conducting the experiment.
• Depending on the desired accuracy, multilateration may be necessary.”
It is clear from the data presented in the First Paper, and more detailed disclosures in a family of patents to Parker and Payne37–40 on the subject, that meaningful NDT and SHM measurements could be made by those more experienced in the use of EDM—such as the members of the CMS and dimensional metrology measurement service providers. Moreover, it is clear that by making high accuracy 3D measurements, the data analysis would be almost intuitively obvious to an experienced structural engineer. This is in direct contrast with the conventional methods of trying to determine the mechanical properties of a structure based on measured accelerations due to vibrations. This assumption is bolstered by articles by Moreu et al.,41–44 in which a survey of 16 railway structural engineers shows that deflection measurements were given the highest ranking for proposed research topics.
It is respectfully submitted that while an argument can be made that the NDT community is largely unaware of the state of the art in coordinate metrology, an argument can also be made that the coordinate metrology community is also largely unaware of the needs of the NDT community. Other than the family of patents to Parker and Payne,37–40 the only other known applications are two patents to Marsh and VanScotter,45,46 which are excellent examples of NDT applications—although on a smaller geometric scale than civil structures. A comprehensive review on laser trackers, in 2016, by Muralikrishnan et al.,47 does not address NDT. The Precision Path Consortium for Large-Scale Manufacturing (PPC)48 is also silent as to NDT applications, and apparently uninterested. An email including comments pointing this out was sent to the PPC members following the CMSC 2016 Conference,49 but was not acknowledged with a response.3
Need for additional instrument specifications
While instruments designed specifically for NDT and SHM will inevitably be built in the future, by current instrument manufacturers or new startup companies, it is postulated that existing commercial instruments are already capable of making useful NDT and SHM measurements. What is needed is recognition by the industry of the potential market and providing some assistance to the early adopters in the NDT field, as well as dimensional metrology measurement service providers working with NDT engineers.
For example, laser trackers and total stations are typically specified for use as a conventional laser-based spherical coordinate measurement system complying with ASME B89.4.19, ISO 10360-10, and ISO17123-5 standards.50–52 These tests are not particularly useful for the NDT community. By providing more useful information about the existing instruments, the NDT community could start learning about the instrument capabilities, writing grant proposals, and performing simple proof-of-principle experiments, with little initial investment by the instrument manufacturers.
The weak link in the 3D coordinate measurement is the angle measurements. If one assumes an instrument will only be used as a conventional single instrument in a 3D coordinate measurement system, there is no need to publish specifications for the distance meter portion, apart from the angle measurement limitations.
If, on the other hand, one were to have an application that lends itself to measuring in only the radial direction, for a 1D measurement, or use a combination of instruments in a trilateration architecture for a 3D measurement, the uninitiated may be led to believe that the range for commercially available instruments is limited to the published 3D specifications, and incorrectly assume the measurement cannot be performed with the instruments available. For example, as shown in table 1, the range specifications for present-day commercially available laser trackers is between 80 m and 160 m.
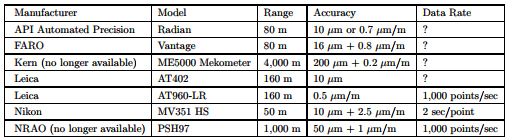
Table 1. Range and accuracy for laser trackers. Click here for larger image.
However, we know this is an artificial limitation. The Kern ME5000 Mekometer,53–55 which is no longer commercially available, has a range of 4,000 m56 with a single prism. Moreover, the ME5000 Mekometer was a revolutionary innovation in dimensional metrology and found many uses—even though it only measured range, i.e., it did not track and lock onto a target to measure the angles. While commercially available total stations can measure similar ranges, they do not have the same accuracy as the ME5000 Mekometer, nor do they have the accuracy of modern laser trackers.
An instrument with the radial distance accuracy of a laser tracker, and an extended range greater than 80 to 160 m would have applications in NDT—even without the angle measurements. This could be an improved accuracy total station, or an extended-range laser tracker—although the distinction between the two has narrowed, since the introduction of the Leica AT401 in 2010. In particular, a range of as little as 1,000 m would probably cover most civil-structure applications.
A recurring theme in the specific examples reviewed in the First Paper13–29 is the desire to measure vertical deflections and vibrations, although an argument can be made that full 3D measurements would be much more useful. In most cases, the experimenters tried to measure these deflections and vibrations using the angle measurements of a total station, i.e., involving image sensors, mechanical systems, motors, and servo systems, in addition to high sensitivity to turbulence and instrument-mounting vibrations—in daylight.
In contrast, the distance meter is ideally suited to measuring dynamic changes in distance in the radial direction, i.e., it is purely an electronic measurement, with no motors and mechanical movement required, and far less sensitive to turbulence and instrument mounting vibrations. This technique has been used in a patent to Nelson et al.,57 to monitor vibrations in machines. Due to the legacy of measurements made in a 3D coordinate measurement system, and the angle measurement limitations, there are no known published specifications for the dynamic measurement capability of the stand alone distance meter subsystem of a laser tracker or total station.
There is not much to be gained by specifying the frequency and amplitude of measurements for a spherically mounted retroreflector resting in a static nest, if the objective is to compare the measurements to static drawing specifications.
If, on the other hand, one wishes to exploit the inherent capabilities of a laser tracker as a dynamic coordinate measurement system (DCMS), all that is required is an understanding of the instrument operations,58–61 and perhaps some software modifications, to make it possible. An argument will be made that laser trackers and total stations should begin to be thought of as DCMS.
If one assumes a movement in the radial direction r to be a sinusoidal function of time t with amplitude a, frequency f, and average distance r0
r = a sin(2πft) + r0 (1)
and the radial velocity v will be, v = a2πf cos(2πft) (2)
which implies the maximum velocity capability needed for measuring vibrations in the radial direction is a2πf.
It may be that simply specifying the maximum velocity the instrument can measure, for a given set of signal processing parameters, would give experimenters a guideline as to the utility of making the measurements with a particular instrument. However, the distance meter architecture may also play a role, e.g., pulse vs. phase measurement, sampling rates, integration time, signal-to-noise ratio, etc., may make the maximum amplitude as a function of frequency highly nonlinear. It may require a chart showing a family of curves of maximum amplitude vs. frequency ranges, for each selected dwell time, to know if an instrument is capable of making a particular measurement.
It should be pointed out that vibration measurements are typically made by accelerometers. For the sinusoidal function in equation 1, the acceleration A would be,
A = −a(2πf) 2 sin(2πft). (3)
Most engineers don’t think in terms of acceleration, which goes back to the analysis problems pointed out by Webb et al.12 above. They would like for the data to quantify what they design for and see, i.e., movements of a structure. Since accelerometers measure acceleration, r must be calculated by integrating the acceleration twice:
![]()
which is prone to error for significant integration time, i.e., the integration leads to drift. EDM measurement has a distinct advantage of being inherently stable for long term trend analysis over the life of a structure, and low frequency vibrations, such as a swaying tower or bridge, and it correlates with motions engineers design for and can visualize, which makes the analysis much easier.
Instrument specifications
Work has been done at the University of North Carolina at Charlotte by Morse and Welty62–64 to dynamically test laser trackers. However, the test uses a rotating ball bar which, due to the geometry, primarily measures the dynamic response of the tracking, angle measurements, and servo system. For an instrument located on the axis of rotation, the distance would not change as the target maps out a cone. In order to modulate the distance, the instrument must be off-axis to map an elliptical motion of the target, which is still primarily a test of the servo system. Moreover, the axis offset is limited by the acceptance angle of the rotating target.
Another test method is disclosed in a patent to Parker,65 which uses a harmonic oscillator, such as a plane pendulum, vibrating beam, torsional balance, etc., to produce uniform motions that can be configured to be primarily along the radial direction, or alternately, primarily in the direction of the azimuth or elevation angles, which facilitates a simple test of each component. A field test using an oscillator with a period of 0.3 seconds can be as simple as attaching a retroreflector to a meter stick and suspending the meter stick using a razor blade for a knife edge bearing, to construct a pendulum. The meter stick can also be clamped in a vice, and plucked, to produce a higher frequency damped oscillator.
Table 2 shows information that would be useful for an engineer designing an experiment using a laser tracker distance meter. The list and values are merely exemplary and may depend on the architecture of the instrument, e.g., pulse vs. phase measurement. Most of the items are self-explanatory, but some are not obvious.
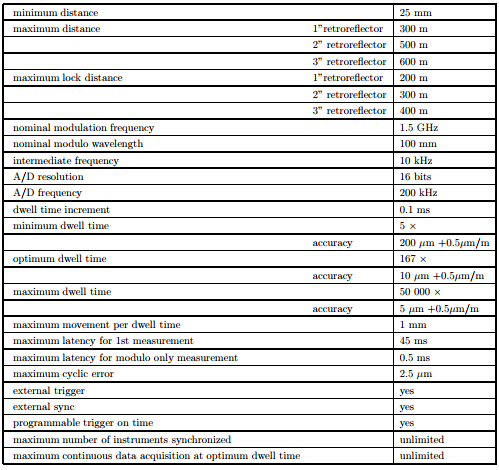
Table 2. Example radial distance measurement specifications. Click here for larger image.
Some instruments have a minimum distance requirement. The maximum distance may depend on the return power, so it may depend on the retroreflector size. Even if the angle measurements are not to be used, one needs to know the maximum distance the servo will lock onto the retroreflector in order to maintain a strong return signal.
For a phase measurement system, one would like to know the nominal modulation frequency, i.e., the frequency at which the laser is modulated for the most accurate measurement, as opposed to the temporary frequencies used to resolve the initial absolute distance ambiguity. This determines the nominal modulo wavelength over which the phase is measured.
The return signal is typically mixed down to an audio frequency intermediate frequency (IF) for the phase measurement, i.e., the frequency of the signal at the A/D converter. A series of samples are made synchronously for each period of the IF, which are used to calculate the phase, using a digital signal processing technique.66–69
For example, if the IF is 10 kHz and it is determined that 20 samples should be made over the period of one cycle, the sampling frequency would be 200 kHz.
Depending on the signal-to-noise of the instrument, and the atmospheric turbulence, a series of periods are averaged to determine the phase. The dwell time must be integer multiples of the period of the IF, so for an IF of 10 kHz, the dwell time increment would be 0.1 ms. Other dwell times must be integer multiples of 0.1 ms. For example, the minimum dwell time may be five times the dwell time increment, or 0.5 ms. For enhanced accuracy, the dwell time may be increased to average out noise. For example, it may be useful to average over multiples of 16.67 ms in order to reduce 60 Hz noise. Of course, that would limit the vibration frequency being measured to under 30 Hz.
In some cases, it may be more useful to specify the maximum movement ∆r between sequential measurements ∆t to a fraction of the nominal modulo wavelength, e.g., 1 percent.
For NDT applications, it may be desirable to measure a plurality of targets attached to the structure by switching rapidly between the targets in a sequence. For example, measuring 10–20 targets per second. When switching to a new target, the instrument typically switches through a series of modulation frequencies to resolve the absolute distance ambiguity, which is a maximum latency for the first absolute distance measurement. However, for quasi stationary targets, such as on a bridge, there is no need to repeat the full ambiguity measurement every time the instrument switches to the target, so the instrument can make the first measurement immediately after switching with a much shorter maximum latency. For some measurements, the experimenter may only be interested in the AC component and there is no reason to make the absolute distance measurement at all.
There is typically a small cyclic error due to multiple reflections back from the instrument to the retroreflector.56,70 For some experiments, data acquisition may need to be synchronized to an external trigger and multiple instruments may need to by synchronized so the IF signals are synchronized. Some experiments may want to preprogram the data acquisition based on absolute time.
References
1. Parker, D. H. “Nondestructive testing and monitoring of stiff, large-scale structures by measuring 3D coordinates of cardinal points using electronic distance measurements in a trilateration architecture.” Conference on nondestructive characterization and monitoring of advanced materials, aerospace, and civil infrastructure 2017, Portland, OR. Proceedings of SPIE 10169, pp. 1016918–1 through 20, 2017.
2. Fuchs, P. A. and S. B. Chase. “Bridge virtual assembly system for steel bridge fabrication.” Transportation Research Board annual meeting 2017. Jan. 2017 paper 17-03603, abstract only.
3. Fuchs, P. A. “Instrument to Aid in Steel Bridge Fabrication.” Final report of Highway IDEA Project 127. Transportation Research Board, March 2009.
4. Fuchs, P. A. “Bridge Retrofit Laser System.” Final report for Highway IDEA Project 153. Transportation Research Board, Sept. 2012.
5. Fuchs, P. A. “Apparatus and method for bridge assembly,” 2014. U.S. Patent Application Publication 2014/0207410.
6. Pettersson, B. “Method and system for virtual assembly of a structure,” 2015. U.S. Patent Application Publication 2015/0254376.
7. Marsh, B. J.; T. Vanderwiel; K. VanScotter; M. Thompson. “Method for fitting part assemblies,” July 2010. U.S. Patent 7,756,321.
8. Marsh, B. J.; VanScotter, K. D.; K. Malen-Hogle. “Splicing fuselage sections without shims,” Aug. 2010. U.S. Patent 7,787,979.
9. B. J. Marsh, K. D. VanScotter, and K. Malen-Hogle. Splicing fuselage sections without shims,” June 2011. U.S. Patent 7,957,825.
10. Ettouney, M. M. and S. Alampalli. Infrastructure Health in Civil Engineering, Volume 1: Theory and Components. CRC Press, 2012.
11. Ettouney, M. M., and S. Alampalli. Infrastructure Health in Civil Engineering, Volume 2: Applications and Management. CRC Press, 2012. 8.
12. Webb, G. T.; P. Vardanega; C. R. Middleton. “Categories of SHM deployments: technologies and capabilities,” Bridge Engineering 20, pp. 04014118–1 through 15, Nov. 2015.
13. Cosser, E.; G. W. Roberts; X. Meng; A. H. Dodson. “Measuring the dynamic deformation of bridges using a total station,” Proceedings of 11th FIG Symposium on Deformation Measurements, Santorini, Greece. The International Federation of Surveyors (FIG), 2003.
14. Merkle, W. and J. J. Myers. “Use of the total station for serviceability monitoring of bridges.” Proceedings of 16th WCNDT 2004. World Conference on NDT, Montreal, Canada, 2004.
15. Matta, F.; F. Bastianini; N. Galati; P. Casadei; A. Nanni. “In-situ load testing of Bridge A6358 Osage Beach, MO,” Tech. Rep. UTC R124-3, University Transportation Center Program, The University of Missouri-Rolla, Jan. 2005.
16. Galati, N.; P. Casadei; A. Nanni. “In-situ load testing of Bridge A6101 Lexington, MO,” Tech. Rep. UTC R124-1, University Transportation Center Program, The University of Missouri-Rolla, Jan. 2005.
17. Hernandez, E.; N. Galati; A. Nanni. “Assessment of bridge technologies through field testing: In-situ load testing of Bridges B-20-133 and B-20-134, Fond du Lac, WI.” Tech. Rep. UTC R133A, University Transportation Center Program, The University of Missouri-Rolla, Dec. 2005.
18. Hernandez, E.; N. Galati; A. Nanni. “Assessment of bridge technologies through field testing: In-situ load testing of Bridges B-20-148 and B-20-149, Fond du Lac, WI.” Tech. Rep. UTC R133B, University Transportation Center Program, The University of Missouri-Rolla, Dec. 2005.
19. Galati, N.; P. Casadei; A. Nanni. “In-situ load testing of Bridge A6102 Lexington, MO.” Tech. Rep. UTC R124-2, University Transportation Center Program, The University of Missouri-Rolla, Jan. 2005.
20. James, H. “Automatic deformation monitoring.” The American Surveyor, March/April 2006.
21. Gikas V. and S. Daskalakis. “Full-scale validation of Tracking Total Stations using a long stroke electrodynamic shaker.” Proceedings of 23th International FIG Congress. Munich, Germany, 2006.
22. Palazzo, D.; R. Friedmann; C. Nadal; M. S. Filho; L. Veiga; P. Faggion. “Dynamic monitoring of structures using robotic total station.” Proceedings of 23th International FIG Congress, Munich, Germany, Oct. 2006.
23. Umemoto, S.; T. Hara; K. Kubota; N. Miyamoto; Y. Fujino; T. Okamoto. “Verification of high-accuracy and contact measurement system using FSF laser optical coordinate.” Proceedings of the Third International Conference on Structural Health Monitoring of Intelligent Infrastructure, Vancover, British Columbia, Canada, Nov. 2007.
24. Kopáčik, A.; P. Kyrinovič; I. Lipták; J. Erdély. “Automated monitoring of the Danube Bridge Apollo in Bratislava.” Proceedings of the FIG Working Week 2011, “Bridging the Gap Between Cultures,” Marrakech, Morocco, May 2011.
25. Attanayake, U.; P. Tang; A. Servi; H. Aktan. “Noncontact bridge deflection measurement: Application of laser technology.” Proceedings of the International Conference on Structural Engineering Construction and Management (ICSEM), 2011, Peradeniya, Sri Lanka, 2011.
26. Psimoulis P. and S. Stiros. “Using robotic theodolites (RTS) in structural health monitoring of short-span railway bridges.” Proceedings of 1st Joint International Symposium on Deformation Monitoring, Hong Kong, China, The International Federation of Surveyors (FIG) Working Group 6.1—“Deformation Measurement and Analysis”; and The International Association of Geodesy (IAG) Sub-Commission 4.2—“Applications of Geodesy in Engineering,” FIG, 2011.
27. Barazzetti, L.; A. Giussani; F. Roncoroni; M. Previtali. “Monitoring structure movement with laser tracking technology.” Proceedings of SPIE—“Videometrics, Range Imaging, and Applications XII” and “Automated Visual Inspection,” 8791, pp. 879106–1 through 12, SPIE, 2013.
28. Psimoulis, P. A.; I. Peppa; L. Bonenberg; S. Ince; X. Meng. “Combination of GPS and RTS measurements for the monitoring of semi-static and dynamic motion of pedestrian bridge.” Proceedings of Third Joint International Symposium on Deformation Monitoring, Vienna, Austria, Joint International Symposium of The International Federation of Surveyors (FIG) Working Group 6.1, Deformation Measurement and Analysis and The International Association of Geodesy (IAG) Sub-Commission 4.2—“Applications of Geodesy in Engineering,” FIG, 2016. 9.
29. Marendić, A.; R. Paar; I. Grgac; D. Damjanović. “Monitoring of oscillations and frequency analysis of the railway bridge ‘Sava’ using robotic total station.” Proceedings of Third Joint International Symposium on Deformation Monitoring, Vienna, Austria, The International Federation of Surveyors (FIG) Working Group 6.1—“Deformation Measurement and Analysis” and The International Association of Geodesy (IAG) Sub-Commission 4.2—“Applications of Geodesy in Engineering,” FIG, 2016.
30. Liu, W.; S. Chen; D. Boyajian; E. Hauser. “Application of 3D LIDAR scan of a bridge under static load testing.” Materials Evaluation 68, pp. 1359–1367, Dec. 2010.
31. Dai, K.; C. Watson; W. Liu; S. Chen; E. Hauser. “Validation of bridge deflection measurements using LiDAR scan.” Proceedings of conference on Structural Materials Technology 2010, pp. 236–244, American Society for Nondestructive Testing, 2010.
32. Brunkhorst, M. “GEO-5626: Building Europe’s mightiest lift bridge.” Proceedings of Trimble Dimensions Conference, Las Vegas, NV, 2014. PowerPoint presentation.
33. Trunick, P. A. “A tale of two bridges.” Point of Beginning, pp. 8–11, February 2017.
34. Flanigan, K. A.; N. R. Johnson; R. Hou; M. Ettouney; and J. P. Lynch. “Utilization of wireless structural health monitoring as decision-making tools for a condition and reliability-based assessment of railroad bridges.” Proceedings of Conference on Sensors and Smart Technologies for Civil, Mechanical, and Aerospace Systems 2017; Proceedings of SPIE 10168, pp. 101681X–1 through 17, 2017.
35. Rakoczy, A. M.; X. Shu; and D. Otter. “Vehicle-track-bridge interaction modeling and validation for short span railway bridges.” Proceedings of Transportation Research Board 2017 Conference, 2017.
36. Taghinezhad, R.; J. H. Gull; H. Pham; L. D. Olson A. Azizinamini. “Acoustic emission monitoring during the deconstruction of a post-tensioned segmental bridge: Case study.” Proceedings of Transportation Research Board 2017 Conference, 2017.
37. Parker, D. H. and J. M. Payne. “Method for measuring the structural health of a civil structure,” 2011. U.S. Patent 7,895,015.
38. Parker, D. H. and J. M. Payne. “Methods for modeling the structural health of a civil structure based on electronic distance measurements,” 2012. U.S. Patent 8,209,134.
39. Parker, D. H. and J. M. Payne. “Methods for measuring and modeling the structural health of pressure vessels based on electronic distance measurements,” 2016. U.S. Patent 9,354,043.
40. Parker, D. H. and J. M. Payne. “Methods for measuring and modeling the process of prestressing concrete during tensioning/detensioning based on electronic distance measurements,” 2016. U.S. Patent Application Publication 2016/0274001.
41. Moreu, F. J.; M. LaFave; B. F. Spencer. “New regulations on railroad bridge safety: Opportunities and challenges for railroad bridge monitoring.” Proceedings of SPIE—“Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2012,” 8345, pp. 834540–1 through 11, 2012.
42. Moreu, F. and J. M. LaFave. “Current Research Topics: Railroad Bridges and Structural Engineering.” NSEL Report Series, Report No. NSEL-032. Newmark Structural Engineering Laboratory, Department of Civil and Environmental Engineering, University of Illinois at Urbana-Champaign, Oct. 2012.
43. Moreu, F.; H. Jo; J. Li; R. E. Kim; S. Cho; A. Kimmle; S. Scola; H. Le; B. F. Spencer Jr.; J. M. LaFave. “Dynamic assessment of timber railroad bridges using displacements.” Journal of Bridge Engineering, p. 04014114, 2014.
44. Moreu, F.; J. Li; H. Jo; R. E. Kim; S. Scola; B. F. Spencer Jr.; J. M. LaFave. “Reference-free displacements for condition assessment of timber railroad bridges.” Journal of Bridge Engineering, p. 04015052, 2015.
45. Marsh, B. and K. VanScotter. “Flight in Factory,” March 2010. U.S. Patent 7,672,817.
46. Marsh, B. J. and K. VanScotter. “Flight in Factory,” April 2014. U.S. Patent 8,688,408.
47. Muralikrishnan, B.; S. Phillips; D. Sawyer. “Laser trackers for large-scale dimensional metrology: A review.” Precision Engineering 44, pp. 13–28, 2016.
48. “Precision Path Consortium for Large-Scale Manufacturing.” Advanced Manufacturing Technology Consortia (AMTech) grant from the National Institute of Standards and Technology (NIST) http://precisionpathconsortium.com/. 10.
49. Parker, D. H. “Comments on Precision Path Consortium.” Email sent to Precision Path Consortium chairman for distribution to members, Aug. 15, 2016. Copy available on request to david@parker-ip-ent.com., Aug. 2016.
50. The American Society of Mechanical Engineers. ASME B89.4.19-2006—“Performance evaluation of laser-based spherical coordinate measurement systems,” 2006.
51. ISO. ISO 10360-10—“Geometrical product specifications (GPS)—Acceptance and reverification tests for coordinate measuring systems (CMS)—Part 10: Laser trackers for measuring point-to-point distances,” first ed., 2016.
52. ISO. ISO 17123-5—“Optics and optical instruments—Field procedures for testing geodetic and surveying instruments—Part 5: Total stations,” second ed., 2012.
53. Bell, B., ed., Proceedings of the workshop on the use and calibration of the Kern ME5000 Mekometer, Stanford Linear Accelerator Center, June 1992. Prepared for the Department of Energy under contract number DE-AC03-76F00515.
54. Mihorko, Katja. Elektronski razdaljemer. YouTube, April 2013. https://www.youtube.com/watch?v=j0uk3cIufQ0.
55. UPV Radiotelevisio. “Noticias destacadas.” YouTube, Nov. 2012. https://www.youtube.com/watch?v=OFuhFBiTV3o.
56. Rüeger, J. M. Electronic Distance Measurement, Springer-Verlag, third ed., 1990.
57. Nelson, M. A.; N. S. Iyer; J. E. Hershey; C. E. Seeley; P. P. Bonissone; K. F. Goebel. “System and methods for remote monitoring of vibrations in machines,” Feb. 2010. U.S. Patent 7,667,827.
58. Meier, D. “Electro-optical measuring device for absolute distances,” 1998. U.S. Patent 5,764,360.
59. Bridges, R. E.; L. B. Brown; J. K. West; D. S. Ackerson. “Laser-based coordinate measuring device and laser-based method for measuring coordinates,” 2010. U.S. Patent 7,800,758.
60. Meier, D.; R. Zumbrunn; T. Jensen; B. Braunecker. “Coordinate measurement instrument,” Oct. 2011. U.S. Patent 8,031,331.
61. Stempfhuber, W. “Verification of the trimble Universal Total Station (UTS) performance for kinematic applications.” Proceedings of Optical 3D Measurement Techniques IX, Vienna, Austria, pp. 211–221, 2009.
62. Morse, E. P. and V. Welty. “Evaluation of dynamic measurements with laser trackers.” Proceedings of CMSC Conference 2013, San Diego, CA, July 2013.
63. Morse, E. P. and V. Welty. “Dynamic testing of laser trackers.” CIRP Annals of Manufacturing Technology, April 2015.
64. Welty, V. “Dynamic evaluation of laser trackers.” Master’s thesis, University of North Carolina at Charlotte, 2015.
65. Parker, D. H. “Method for calibrating a laser-based spherical coordinate measurement system by a mechanical harmonic oscillator,” 2010. U.S. Patent 7,856,334.
66. Payne, J.; D. Parker; R. Bradley. “Rangefinder with fast multiple range capability.” Review of Scientific Instruments 63, pp. 3311–3316, June 1992.
67. Payne, J.; D. Parker; R. Bradley. “Rangefinder with fast multiple range capability,” Selected Papers on Laser Distance Measurements, SPIE Milestone Series MS 115, T. Bosch and M. Lescure, eds., pp. 257–262, SPIE Optical Engineering Press, 1995. reprint of Review of Scientific Instruments article.
68. Bridges, R. E. and J. M. Hoffer. “Absolute distance meter that measures a moving retroreflector,” 2008. U.S. Patent 7,352,446.
69. Bridges, R. E. and J. M. Hoffer. “Absolute distance meter that measures a moving retroreflector,” 2010. U.S. Patent 7,701,559.
70. Burnside, C. D. Electromagnetic Distance Measurement, BSP Professional Books, third ed., 1991. 11.
Add new comment