Recent interest in portable coordinate measuring systems (CMS) has attracted the attention of industrial users and the technical community at large. Articulated arm coordinate measuring machines (CMMs) and optically tracked CMM (OTCMM) systems have emerged from being “nice-to-have” to “must-have” 3D equipment on the shop floor.

Portability and flexibility for in-process product measurements and verification are displacing more traditional methods that require fixed gantries, especially when OTCMM are combined with tracking devices that can compensate for vibration levels of a typical shop floor. The current set of recognized contact CMS standard documents produced by ISO, VDI, ASME organizations cover fixed-gantry CMMs. However, these standards cover one class of OTCMM (i.e., laser trackers) and neglect the class of OTCMM that include spherical-stylus touch probes tracked by contrast targets-based optical triangulation methods. It is within this context that we propose a harmonization scheme for terminology, discuss test methods complemented with experimental data, and reference artifacts for the purpose of ensuring comparability of CMS and helping in pre-normative documentary/physical standards definition.

Introduction

Market data shows an increasing interest in using portable CMS for shop floor measurement tasks (Frost 2016). They have attracted the attention of industrial users and the technical community at large, which is accustomed to using fixed CMS, e.g., gantry-type CMMs, also known as cartesian CMS. The documentary and physical standards produced to date can help companies that integrate contact or noncontact CMS into their production pipeline. Many more aspects need to be addressed; in particular, CMS involve a significant investment when considering the cost of equipment, training, software, and maintenance contracts over the functional lifetime of a given system or systems, notwithstanding the requirements of the global nature of manufacturing activities. This article summarizes the results of experiments using two portable contact non-Cartesian CMS (see figure 1a, b, and c). The laboratory and shop floor experiments were based on ASME B89.4.22-2004-R2014, VDI/VDE 2617 Blatt 9:2009, and ISO 10360-12. It is within this context that we propose a harmonization scheme for terminology, discuss test methods complemented with experimental data performed in a laboratory and a shop floor including vibrations, and increase awareness in normative activities for OTCMM.

Figure 1: Portable CMS used in the study: a) Articulated arm CMM (AACMM) with hard probe, b) Optically tracked CMM (OTCMM) with target-based probe, c) OTCMM global view, and d) Kinematic seat with the spherical probe.

We present preliminary results of an evaluation of an OTCMM system (see figure 1b, c). These results are compared to those obtained using an AACMM (see figure 1a). This comparison will help the reader already familiar with the AACMM to see parallels with current practices and combines all test methods into a common body of knowledge for portable CMS. We draw methods from current standards to create test methods and adapt them to the particular characteristics of OTCMM.

Background

Classification of CMS

The term CMS is proposed to describe any measurement system that generates triplets of (x, y, z) numbers or three-dimensional (3D) coordinates that represent a surface of an object. These coordinates are acquired by touching the surface (contact probing) or by a light-based technique (i.e., noncontact probing). Contact probing is typically used on a CMS with a small sphere attached to a stylus. Noncontact measurement is achieved using light-based methods such as lasers or white-light projectors. Using optical triangulation, a laser beam can produce a set of 3D coordinates, or a point cloud, which contains millions of 3D coordinates (Hocken and Pereira, 2011, Luhmann et al. 2013, Pears et al. 2012).

Many classifications exist depending on user applications and preferences. Here we propose one classification that divides the different techniques into two main categories: Cartesian and non-Cartesian machines. Figure 2 shows the classification and terminology proposed in this article. Most of these CMS are covered by many documentary standards published by ISO, ASME, and VDI/VDE. Noncontact 3D imaging systems are included in documentary standards but consist of acceptance and reverification procedures that follow their contact-based systems counterparts, often neglecting their imaging properties (Beraldin et al., 2015).

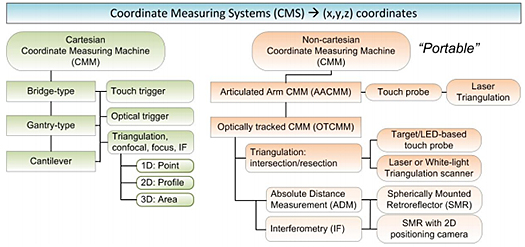
Figure 2: Proposed classification of CMS divided into contact and noncontact methods.

As noted by Philips 2013, CMS are 3D coordinate-collecting instruments but do not deliver a measure of “geometry”, e.g. plane, sphere, etc. These 3D coordinates form the basis of an inspection plan that requires individual 3D points, or inferred 3D points, which are then used in a fitting process (e.g., sphere center), for datum determination, in polygonal model creation, for measuring the deviations of a point cloud with respect to a reference surface, for geometric dimensioning and tolerancing (GD&T), etc. The accuracy of CMS is determined by the 3D point coordinate uncertainty, which varies in magnitude at different locations in the CMS work zone, and depends on the probing approach direction and many other factors.

Portable CMS tested

Tethered systems (i.e., a stylus attached to the motion-tracking arm) encompass AACMM (Romer/Cimcore 5030) and untethered (stylus not attached to the motion tracking system), OTCMM (Creaform HandyPROBE Next|Elite). AACMM use only joint-angle encoders and arm-segment lengths to calculate the position and orientation (pose) of the stylus (see figure 1). The OTCMM described (Larue et.al. 2012) uses triangulation (video/photogrammetry) combined with high-contrast targets to reduce the effect of vibrations found on a typical shop floor. The update rate of the multiple targets extraction is 80 frames per second. Figure 1b and c show a touch-probe system linked to the photogrammetric tracking system. Reflective targets are detected in the two image sequence pair by image processing algorithms. Their 2D positions on the array (2D) cameras are then used in a 3D triangulation process (photogrammetric intersection) to estimate the 3D center coordinate of each reflective target. Sets of 3D coordinates are then used to compute the pose of the probe, the scanner, and the part on which the reflective targets are affixed. The measurement volume of portable systems can be extended though accurate repositioning or multiple tracking-device installation by leap-frogging for low-accuracy applications and photogrammetry for global accuracy retention. The measurement volume of an OTCMM based on two array cameras is a truncated cone (see figure 3). Because this category of portable CMS is not covered by many technical articles in an extensive way (Lau et. al. 2010, Muralikrishnan et. al. 2015) and has not seen any significant normative activity, we plan to test a system using the B89.4.22-2004 as a baseline standard and add other tests such as vibration analysis.

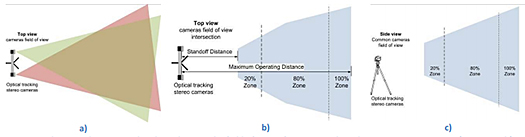
Figure 3: Schematic diagram on the plane showing the field of view of an OTCMM based on two array cameras: a) top view, b) top view showing the results of the intersection of the cameras’ field of view, c) the side view. (Not to scale)

Current ISO, ASME standards, and VDI guidelines

The ASME B89.4.22-2004 standard proposes three methods for performance evaluation: effective diameter performance test (EDT), single-point articulation performance test (SPAT), and a volumetric performance test (VT). Furthermore, it provides definitions, design and mounting recommendations, and environmental requirements. The appendices contain non-mandatory information so it is strongly recommended that the user read through them to understand the best practices they contain.
• Effective diameter performance test (EDT). This test is designed to reveal problems such as excessive machine or probe hysteresis, or improper probe calibration. A single 10 mm to 50 mm diameter calibrated sphere (see figure 4a) is measured with nine well-distributed probing points. The same location (in the middle of the reach of the arm) of a rigidly-mounted sphere is measured three times and the largest test deviation from the calibrated diameter value is reported regardless of the sign. During the test, the articulations of the AACMM are minimized for each measurement. An unconstrained least-squares fitting method is used to obtain the diameter of the measured sphere and the Gaussian regression sphere. The estimated diameter and calibrated diameter are then compared. The combined sphericity (roundness) and surface finish of the calibrated sphere should not exceed 1/3 of the working tolerance for the single-point articulation performance test. The standard explains the procedure to remove outliers.
• Single-point articulation performance test (SPAT). The test assesses the AACMM’s ability to provide similar values of a point coordinate when its encoders and segments are exercised through a large range of motion to acquire a point. When using a kinematic seat (figure 1d), the artifact is measured at three locations: within 20 percent, between 20 percent and 80 percent, and between 80 percent and 100 percent of the length of the arm. It is important to break the contact between the artifact and the probe at each probing point. For each position, the arm is articulated through ten orientations. A point is measured at each of the ten arm orientations. The statistics reported are the maximum deviation of the points from a mean value and twice the standard deviation of the point location. These two results provide a measure of the combined variability in the three mutually perpendicular axes. The explanation is often misinterpreted on specification sheets published by some manufacturer, which report results only along one axis! The standard explains the procedure to remove outliers.
• Volumetric performance test (VT). The measurement volume of an AACMM is spherical so this test can’t separate errors in a Cartesian coordinate system. Aspects of the linear displacement accuracy, as described in Cartesian CMM and volumetric performance tests, are combined to form the volumetric performance test. This combined performance is evaluated using two calibrated length artifacts, each composed of two gauge features (e.g., kinematic seat). The length artifact, with suitable thermal correction, is placed in at twenty orientations: two vertical orientations, ten horizontal orientations, and eight 45° orientations. The operator must record five measurement points per gauge feature. The standard describes two length artifacts; the first is 50 percent to 75 percent, and the second is 120 percent to 150 percent of the radial length of the AACMM arm. The default length artifact is the ball bar (see figure 4b). The length deviation from the calibrated value is computed and the results of this test are reported as three quantities: the maximum deviation, the range of the deviations, and two times the RMS of deviations. The standard explains the procedure to remove outliers.

Figure 4: Calibrated artifacts: a) calibrated sphere, b) cantilever ball bar with kinematic mounts used to limit the orientation of the bars (limiting pin shown) and long gauge block (top of photograph).

German guideline VDI/VDE 2617 Blatt 9 applies to the acceptance tests used to verify conformance of the AACMM to the manufacturer’s specifications, and the reverification tests performed by the user for periodic checking of the AACMM. Calibrated artifacts are referred to in the guideline as calibrated material measures. Both probing error and errors of indication for size measurement are included in the tests. Because of the manual operation of the probe, the guideline explicitly mentions that fewer measurements are to be performed compared to the case of a Cartesian CMM. The first test is designed to evaluate the size, form, and location of a standard sphere whose nominal diameter varies between 10 mm and 50 mm, and whose form and size (diameter) are calibrated (less than 20 percent of the MPE for form). Evaluations are performed at three different positions in the measuring volume: one at 30 percent from AACMM location, one in the 30 percent to 70 percent range and one from 70 percent to the reachable useful arm length. At each position, five distributed points on a hemisphere of the sphere are probed. The operation is repeated five times using different stylus orientations. A total of 75 points are measured, and for each group a Gaussian regression sphere using a least-squares fit is performed. Probing error for the sphere location (centers), for the size (known diameter) and the form (spread of known radii) are reported using the largest value method. The second test assesses the geometrical accuracy by performing size measurements using at least five lengths along a measuring line. These lengths must be calibrated and the longest length equal at least 66 percent of the useful measuring range. The calibrated lengths are measured in at least seven poses, which can be chosen arbitrarily by the user. The measurements are repeated three times for a total of no less than 105 measurements. The extreme positions of the arm should be engaged to reveal hysteresis effects. The guideline explains the procedure to remove outliers.

One major difference between the ISO 10360-12 standard and ASME B89.4.22-2004 is that ISO 10360-12 also covers laser sensing systems. ISO 10360-12 presents three methods for performance evaluation similar to those described in the B89. The tests are probing size and form errors, articulated location errors, and length measurement errors. For probing size and form errors, a calibrated test sphere is used and the recommended diameter varies between 10 mm and 51 mm. A total of 25 points are probed on the surface of the sphere, and this process is performed at two locations in the volume. A Gaussian sphere using an unconstrained least-squares fit is performed to estimate the errors of indication for form and size. The motion of the arm is restricted in this test. Size and form are calculated from the calibrated sphere diameter and the measured points. In the articulated location errors test, all the articulation joints are exercised. A test sphere is probed five times in five orientations and a Gaussian sphere using an unconstrained least-squares fit is performed. Two locations for the test sphere are selected anywhere in the measuring volume. The five centers are used to compute the articulated location error. For the length measurement errors test, five different calibrated test lengths are required. Each length is measured three times and the results are compared to their respective calibrated value. Seven measurement lines inside the volume are picked with the longest of the five calibrated lengths being at least 66 percent of the diameter of the spherical volume. A total of 105 measurements are used for this test. It is important to understand the distinction between the unidirectional and the bidirectional length-measurement errors.

Effect of the operator/user on the results

A study commissioned by the Coordinate Metrology Society and conducted at the organization’s annual conference, the CMSC, collected measurement results and focused on core knowledge, understanding, and behavioral requirements for portable coordinate metrology equipment. The measurement study report identified the following eight areas as core knowledge and understanding vital to making informed decisions during the measurement process (CMSC 2011): Standards, Traceability, Calibration, Measurement Uncertainty, Understanding Design Requirements, Repeatability and Reproducibility, Questioning, and Attitudes and Behavior. A follow-up study was performed in 2012 on portable coordinate metrology probing equipment with a focus on practical testing (CMSC 2012). In that study, observation results were compiled for a sample of up to 60 participants for articulated arms and laser trackers with a test piece and a motorcycle component. User/operator inquiries about the environmental conditions, work area checks, equipment considerations, and measurement planning were very limited in that close to 80 percent did not ask questions. Some highlights of the 2012 final report include:
• 87 percent did not ask about potential environmental issues
• 73 percent ignored the stability of the setup
• 95 percent chose more than the minimum number of points to measure form

An AACMM evaluation and calibration procedure should be performed in situ to capture how the system is commonly used, including the operator impact on the CMS performance.

Effect of sample size

If one analyzes the different ways features are probed, one sees that for ASME B89.4.22-2004 the requirement is 5 to 9 probed points repeated 3 to 10 times at 3 to 20 different positions. In ISO 10360-12, the requirement is 5 to 25 points on all surfaces in many locations and at many orientations. Using Cohen’s d to evaluate effect size (O'Keefe, 2007) using an a priori power analysis (APPA) (Cohen, 1992), we see that 9 samples (B89.4) provides an effect size of d =1.3 while 25 samples (ISO 10360-12) provides an effect size of d = 0.8 . This assumes a Type I error (false negative) of 1 – α = 0.95 and a Type II error (false positive) of 1 – β = 0.80. According to Cohen, effect sizes 0.8 or larger are considered “large” (Cohen, 1992), meaning that the test is only sensitive to large effects. Both recommended sample sizes result in tests that are only sensitive to large effects. Guideline VDI/VDE 2617 Blatt 9 proposes 5 distributed points in 3 to 7 different positions and locations, repeated 5 times. Manually repeating measurements (probing) of a feature without considering environmental issues and the stability of the setup may lead to unwanted variability in the results. A thorough gauge R&R becomes an attractive solution for in situ work, and documentary standards may be more valuable if tests were added to measure the effect of the operator.

Reference artifacts, instruments and test conditions

The two portable CMS tested are listed in table 1 and the reference artifacts are itemized in table 2. Only the main data from the calibration certificate are listed. The two physical standard lengths (0.9 m and 2 m) are cantilever ball bars fitted with kinematic seats (see figure 4b). A ring gauge and an aluminum casting were added to simulate normal parts measured on a shop floor.

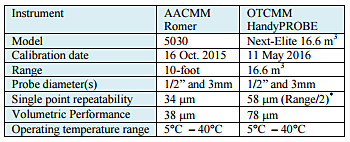
Table 1: List of instruments tested with some of their characteristics.

The reference artifacts listed in the table 2 were measured either in an accredited laboratory in accordance with standard ISO/IEC 17025:2005 or at NRC’s NMI at close to 20°C. This environment is not typical of a shop floor; hence, artifacts need to be corrected for thermal expansion at nonstandard temperatures. The standard length is given by equation 1:

where L_m is the measured length at temperature T, α is the coefficient of thermal expansion (CTE) of the artifact and ΔT is given by (T-20°C). Although this equation seems to indicate that all the factors are constants, this is not the case. Two important sources of uncertainty need to be computed to estimate the uncertainty of the length correction (Doiron and Stoup, 1997).

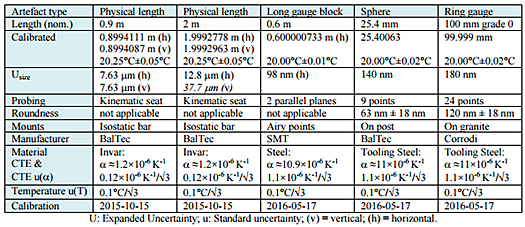
Table 2: List of reference artifacts with some of their characteristics.

The first one comes from the temperature measurement uncertainty, u(T) and the second from the lack of knowledge of the real CTE, u(α). Other sources of uncertainty include probing error and error of indication of size (ISO/TS 23165:2006). The standard uncertainty of the probing error (rigid mounts), u(P), is seen in equation 2:

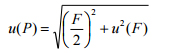
where F is the form error and u(F) is the standard uncer1tainty of the form error from the calibration certificate. The expanded uncertainty U is k x u(P) where k = 2. The equation for the standard uncertainty of the error of indication for size, u(E), is seen in equation 3:

where is the calibration error from the certificate, is the error due to the input value of the CTE, is the error due to the input value of the temperature, is the error due to misalignment, is the error due to fixturing. Two different environments were selected for the tests: laboratory and shop floor. In the laboratory the temperature is maintained at 20º C ± 0.1º C with a relative humidity (RH) of 40 percent to 50 percent year-round; however, we turned off the air conditioning to simulate a rising temperature and variable RH conditions. During the tests the temperature varied between 20º C and 28º C. The second environment was located in the main NRC development shop floor where prototypes are built. The temperature in this location varied between 22º C and 23º C with a lot of air flow and uncontrolled vibrations. An unstable cart (the four legs are not exactly the same length) held the reference artifacts and an artificial source of vibration was used to simulate more realistic situations. Experience shows that in industrial environments some parts are measured directly on shipping crates or wooden pallets. For the tests, the operator was trained by an expert over a period of two days with both systems. The operator performed three repetitions and the maximum value is reported.

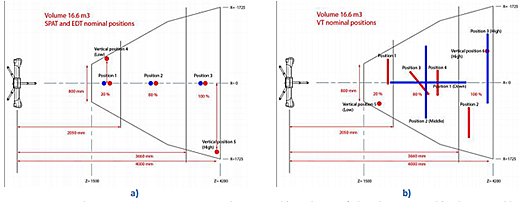
Figure 5: Diagram showing a measurement OTCMM volume viewed from the top: a) Three locations used for the SPAT in blue and five positions for EDT in red, b) Positions of the length artifacts, short length in red and long length (2 m bar) in blue. Click here for larger image.

Test results: Laboratory with air conditioning turned off

Single-point “articulation” performance test (SPAT)

Figure 5a shows a diagram illustrating the three positions of the kinematic nest for the Creaform system. The Romer system was tested according to B89.4.22-2004. The Creaform OTCMM model (16.6 m³) was selected to match the spherical measurement volume of the Romer AACMM as closely as possible. To simulate the “articulation motion” as per B89.4.22-2004, the contrast-target based probe on the Creaform system was placed in different orientations. The interface software informed the operator when the probe was out of range. Dynamic compensation mode was not used. In table 3, we see that the result tends to increase with distance. This is to be expected from a photogrammetric system because the magnification changes with distance. In table 4, we see that the SPAT results tend to be better in the middle 80 percent.

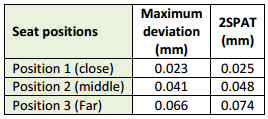
Table 3: SPAT test for the OTCMM. Temperature varied between 21.4° C and 21.7° C.

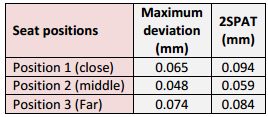
Table 4: SPAT test for the AACMM. Temperature varied between 23.9° C and 24.2° C.

Effective diameter performance test (EDT)

The test is performed with the articulations of the AACMM minimized for the calibrated sphere measurement. The orientation of the OTCMM is minimized to mimic this requirement. Figure 5a shows a diagram with five positions of the sphere for the Creaform system. The Romer system was tested according to B89.4.22-2004. Table 5 gives the results for the Creaform and table 6 for the Romer system, respectively.

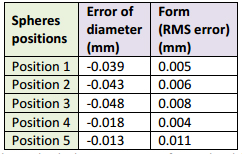
Table 5: EDT results for the OTCMM with a calibrated sphere of 25.4 mm. Temperature varied between 22.0° C and 23.0° C.

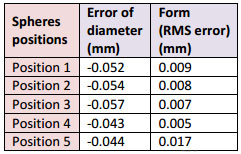
Table 6: EDT results for the AACMM with a calibrated sphere of 25.4 mm. Temperature varied between 24.2° C and 24.7° C.

All of the calculations were performed with the software package PolyWorks Inspector. We used the GD&T controls feature to extract the results in this work. The EDT requires the estimation of the standard uncertainty of the probing error for the calibrated sphere. Using equation 2 and the data from table 2, we get U(P) ≈ 66 nm, which is several orders of magnitude below the RMS fitting errors for both CMS. This probing-error estimate is negligible compared to the fixture-error contribution and the contact probing itself, even if we factor in the CTE. All the measurement errors are negative and indicate either a possible difference in scale between the calibration process of the two CMS and the calibration of the sphere, or a mixture of probe hysteresis and improper probe calibration. This issue is currently being investigated.

Volumetric performance test (VT)

Here we deviate from the prescribed number of test lengths listed in current standards. The long length (2 m nominal) was not tested in the vertical mode because of the high uncertainty from the calibration certificate (table 2). The standard uncertainty of the error of indication of size is calculated with the characteristics listed in table 2 and equation 3. With the long gauge block we get U(E_h) ≈ 0.007 mm, for the nominal length of 900 mm in horizontal and vertical positions we get U(E_h) = U(E_v) ≈ 0.008 mm, and for the 2000 mm length in the horizontal position we get U(E_h) = 0.013 mm. The long gauge block and 900 mm scale bar are shown in figure 4b along with the mounting of the cantilever scale bars. The main source of uncertainty from the long gauge block originates from the uncertainty in the CTE and the temperature variation. For both cantilever scale bars, the calibration process is the main source of uncertainty. The volumetric performance test results are given in table 7 and table 8 and the diagrams on figure 5b and figure 6a.

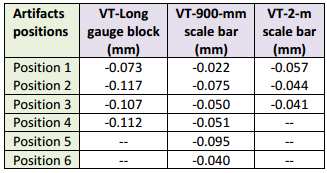
Table 7: Volumetric performance test for the OTCMM. Temperature varied between 27.3° C and 27.9° C.

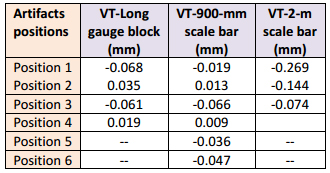
Table 8: Volumetric performance test for the AACMM. Temperature varied between 27.6° C and 27.8° C.

Care was taken to fix the length artifacts on rigid mounts and CTE corrections were applied. The long gauge block was probed with twelve points on each side and two plane equations were fitting assuming parallelism. The scale bars were probed with a 0.5 in. hemispherical anodized-aluminum ball stylus for both CMS. The results indicate again negatives errors for the OTCMM (see table 7). We could not see any trend due to distance between length artifact and optical tracking unit and its orientation. For the AACMM, the results indicate errors that are centered on zero for the short lengths but all negative values for the 2-m scale bar.

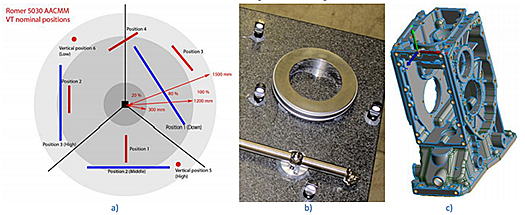
Figure 6: a) VT tests equatorial slice of the volume of the AACMM, b) Ring gauge, c) Aluminum casting.

Optional tests

To verify the performance of the CMS on a typical part, we performed a series of tests on a ring gauge (figure 6b) with a calibration certificate (see table 2). Table 9 and table 10 show the results for both CMS.

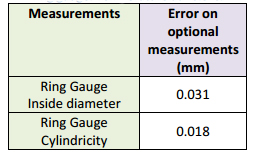
Table 9: Volumetric performance test for the OTCMM on a ring gauge. Temperature at 26.3° C.

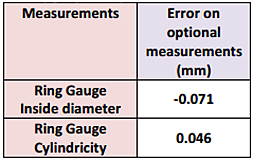
Table 10: Volumetric performance test for the AACMM on a ring gauge. Temperature at 28.9° C.

Test results on a shop floor with vibrations

This section presents the results obtained on a shop floor where the temperature, air flow, and ambient vibrations were not controlled. Additional vibrations were introduced to highlight the tracking features of the OTCMM. Artificial, but repeatable, vibrations were created using a drill spinning an off-axis hex key at low speed attached to the lower portion of a leg of the cart. Both a ring gauge (figure 6b) with a calibration certificate and aluminum cast were measured in the presence of vibrations. The results for the OTCMM operated in dynamic mode (targets tracking mode) are shown in table 11 and for the AACMM that does not have a vibration-compensating mode in table 12. The tests errors without vibration mean that the drill was not turned on and only the table motion produced the vibrations. The tests errors with vibrations were obtained on the table with the drill turned on. Figure 1 shows the photographs of the setup in which retroreflective targets affixed to the artifacts, floor, and cart were tracked using the OTCMM for the dynamic mode operation.

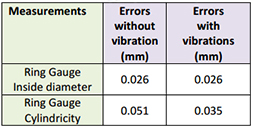
Table 11: Volumetric performance test for the OTCMM on a calibrated ring gauge on the shop floor.

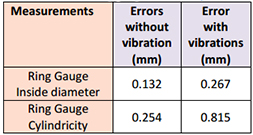
Table 12: Volumetric performance test for the AACMM on a calibrated ring gauge on the shop floor.

On the aluminum cast shown on figure 1b and its CAD model on figure 6c, several features were measured and some results are listed the following two tables. Entries marked “Unable to measure” indicate that many attempts were made to measure these features using the AACMM but the vibrations were too high to obtain any meaningful results. The OTCMM appeared to outperform the system that lacked motion-tracking capabilities.

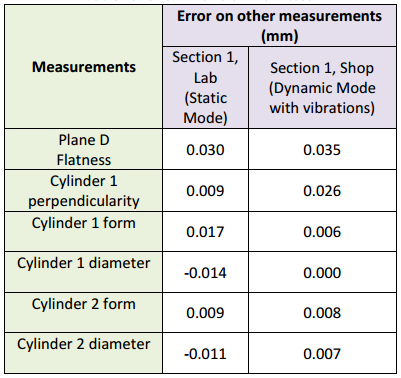
Table 13: OTCMM on aluminum cast.

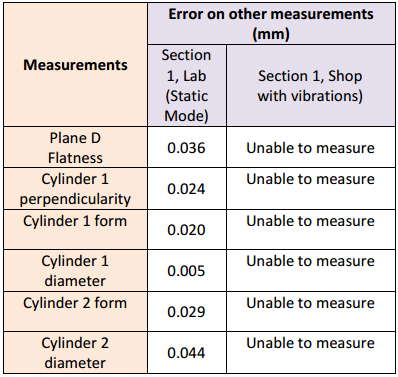
Table 14: AACMM on aluminum cast.

Discussion

The class of portable OTCMM tested in this study has many advantages compared to other CMS, particularly that vibrations and motion that are ubiquitous on shop floors show little effect on measurement results that are used for geometric inspection of parts. Vision systems based on optical-triangulation methods show their versatility and speed when it comes to tracking a contrast target-based spherical-stylus touch probe and many auxiliary contrast targets. The limit on the number of such targets is dictated by the speed of the video cameras and the available processing power. Experimental results indicate that the OTCMM operated close to the value indicated on the calibration certificate, although the temperature varied compared to the conditions existing at time of calibration and the presence of vibrations. In static mode (no target tracking), both CMS gave similar results. The dramatic differences in the quality of the results are clear when vibrations are present. Current terminology, test methods, and reference artifacts are adequate for the purpose of ensuring the comparability of CMS. Future standard activities will need to devise a test method to handle vibrations. In particular, we envision two tests tailored to OTCMM. The first test would use a sphere mounted on a stand that points away from the optical tracking device and would be an effective-diameter test using a 360° all-around measurement with the probe. The second test linked to vibration would require a repeatable and easy way to produce a test based on commercially-available hardware to generate and estimate a set level of vibrations.

At the time of writing, we located a draft standard from the ASTM E57- WK 49831 but were not able to include it in the current study. OTCMM consisting of a stationary optical tracking system and a probe head so may benefit from this future standard. This proposed test method presents metrics and procedures for measuring, analyzing, and reporting the relative pose error of optical tracking systems that compute the pose of an object while the object is moving. Once the final version has been published, a future evaluation of OTCMM systems will include the test procedure and performance evaluation method presented in the standard.

Conclusions

Portable coordinate measuring systems are becoming essential for in-process product measurements and verification because of their portability, versatility, and current level of accuracy. The intent of this article is to raise awareness of a particular class of portable coordinate measuring system that is also attracting the attention of industrial users and the technical community at large, but has not received the same level of technical publications and standard activity as other CMS. The current set of recognized contact CMS standard documents produced by ISO, VDI, and ASME organizations cover CMS; however, these standards don’t cover OTCMM that include spherical-stylus touch probe tracked by contrast targets-based optical triangulation methods. These OTCMM require a new approach to testing and standard definition because they combine tracking devices that can compensate for vibration levels found on a typical shop floor, while the current standards assume a static world. It is within this context that we proposed a harmonized terminology, discussed test methods and showed some experimental data to help in pre-normative documentary/physical standards definition, and stimulate publications on the topic.

Acknowledgments

We wish to thank the members of the NRC-DFS (Mr. Alan Horner) who help to provide an industrial environment to test the dynamic tracking capability of one CMS. InnovMetric Software Inc. has kindly supplied a copy of PolyWorks Inspector for these tests. Creaform kindly provided newly developed commercial versions of HandyPROBE Next|Elite and VXelements software and also a service grade Romer/Cimcore 5030 Articulated Arm for our evaluation of tests methods and future documentary standards. Certain commercial equipment, instruments, or materials are identified in this paper in order to specify the experimental procedure adequately. Such identification is not intended to imply recommendation or endorsement by the National Research Council of Canada, nor is it intended to imply that the materials or equipment identified are necessarily the best available for the purpose.

References

Frost & Sullivan, Analysis of the Global Optical Digitizer and Scanner Market, www.frost.com (last accessed 2016)

B89.4.22 – 2004, Methods for Performance Evaluation of Articulated Arm Coordinate Measuring Machines (CMM), www.asme.org (last accessed June 2016).

VDI/VDE 2617 Blatt 9-2009, Genauigkeit von Koordinatenmessgeräten - Kenngrößen und deren Prüfung - Annahmeund Bestätigungsprüfung von Gelenkarm-Koordinatenmessgeräten, Accuracy of coordinate measuring machines - Characteristics and their reverification - Acceptance and reverification tests for Articulated Arm Coordinate Measuring Machines, www.vdi.de (last accessed June 2016).

ISO/FDIS 10360-12, Geometrical product specifications (GPS) -- Acceptance and reverification tests for coordinate measuring systems (CMS) -- Part 12: Articulated arm coordinate measurement machines (CMM), stage: 50.20/ under development (2016-05-30) www.iso.org (last accessed June 2016).

Hocken, R. J. and Pereira, P. H. (Editors), Coordinate Measuring Machines and Systems, Second Edition (Manufacturing Engineering and Materials Processing) 2nd Edition, CRC Press, July 22, 2011.

Luhmann, T., Robson, S., Kyle, S., Boehm, J., Close-Range Photogrammetry and 3D Imaging, De Gruyter Textbook, 2nd ed. xviii, 2013.

Pears, N., Liu, Y., Bunting, P. (Editors), 3D Imaging, Analysis and Applications, Springer, July 2012.

Beraldin, J.-A., Mackinnon, D. and Cournoyer, L., Metrological characterization of 3D imaging systems: progress report on standards developments, 17th Intern. Congress of Metrology, Paris, France, 2015.

Phillips, S., CMMs, AACMMs, and Laser Trackers: Know the Errors Sources and Improve Accuracy, Presentation at the 2013 NACMA Annual Workshop and Conference, Aug. 27-30, NIST, Gaithersburg, 2013.

Larue, J.-F., Viala, M., Brown, D., Mony, C., Dynamic Referencing in 3D Optical Metrology for Higher Accuracy in Shop Floor Conditions, CMSC Conference, 2012.

Lau, K., Yang, Y., Liu, Y., and Song, H., Dynamic performance evaluation of 6D laser tracker sensor, PerMIS '10 Proc. of the 10th Performance Metrics for Intelligent Systems Workshop, ACM New York, NY, USA 2010, pp. 285-289.

Muralikrishnan, B., Blackburn, C., Rachakonda, P., and Sawyer, D., Performance evaluation of a laser tracker hand held touch probe, Proc. of the Annual Meeting of the ASPE 2015, Austin, TX, November 2-5, 2015.

Bevan, K. and Toman, T., How Behavior Impacts Your Measurement, in CMSC 2011, Report, 2011.

Bevan, K., Toman, T. and Gruver, R., The Importance of Practical Testing, in CMSC 2012, Report, 2012.

O'Keefe, D. J., Brief report: Post Hoc Power, Observed Power, A Priori Power, Retrospective Power, Prospective Power, Achieved Power: Sorting Out Appropriate Uses of Statistical Power Analysis, Communications Methods and Measures, vol. 1, no. 4, pp. 291-299, 2007.

Cohen, J., A Power Primer, Psychological Bulletin, vol. 112, no. 1, pp. 155-159, July 1992.

Doiron, T. and Stoup, J., Uncertainty and Dimensional Calibrations, J. Res. Natl. Inst. Stand. Technol. 102, 647, 1997.

ISO/TS 23165:2006 Geometrical product specifications (GPS) - Guidelines for the evaluation of coordinate measuring machine (CMM) test uncertainty. www.iso.org (last accessed June 2016).

ASTM E57: Subcommittee E57.02 on Test Methods-WK49831 New Test Method for Measuring the Performance of Optical Tracking Systems that Measure Static and Dynamic Six Degrees of Freedom (6DOF), Pose. https://www.astm.org/COMMIT/SUBCOMMIT/E5702.htm (last accessed June 2016).