To demonstrate that a typical spacecraft reflector is designed and manufactured according to specifications and caters to postulated performances, a detailed testing and verification campaign must be conducted. 3D metrology plays an important role in this process.
|
ADVERTISEMENT |
Conventional coordinate measuring machines (CMM) were used to measure the 3D coordinates of thousands of points on the surface and generate a reference on tooling targets mounted on the reflector’s circumference. The measured points are then compared with the theoretical points on the design surface to validate the realized surface.
During the past few decades close-range photogrammetry (CRP) has become popular because of its compactness and accurate measurements. In practical applications, circular retroreflective targets are stuck on the surface under consideration. CRP measures the 3D coordinates of the centroid of these targets, and thereby provides the 3D shape information of the surface.
The measurements carried out on a freeform surface of a reflector using the CMM and CRP has no correlation except the tooling balls. Thus the accuracy comparison for a freeform surface is an inherent question. Traditionally best-fit root mean square (RMS) is the preferred mathematical tool for comparing the surfaces obtained from scanned point clouds. However, fitting a surface using fewer sampled points obtained by CRP and the CMM does not provide a true comparison (RMS difference) between two measurements. Therefore, point-to-point comparison is required.
Three different case studies were carried out to compare the point-to-point accuracies obtained in measuring the reflector surface using CRP and the CMM. This article contains details of the procedures followed and the observations made during the case studies.
Introduction
ISRO Satellite Centre (ISAC) is India’s national organization engaged in designing and building spacecraft. The facilities at ISAC are used for integrating and testing a wide variety of satellite systems for remote sensing and communication applications, and cover a wide frequency range.
Recently, a new thermo-elastic distortion measurement (TED) facility was augmented to study the effects of temperature gradient on the spacecraft reflector inside a climatic chamber (as seen in figure 1). CRP is a well-established technique used worldwide to measure the distortion of surfaces during TED tests. (See references 1–4, below.)

Figure 1: Spacecraft moving inside climatic chamber
Before a TED test is carried out, a number of sampled points on the reflector’s surface are measured using the CMM. The measured points are compared with the theoretical points on the design surface. Also, a RF surface is generated (using interpolation techniques) with these measured points to check for the anticipated gain-to-noise temperature (G/T) and the effective isotropic radiated power (EIRP) of the antennae.
Once these references are established and the reflector design is validated, the reflector is sent for TED tests inside a climatic chamber. Taking a CMM measurement inside the climatic chamber after every cycle (hot or cold) is an inconceivable task. Therefore, CRP was used, and approximately 1,500 to 2,000 targets were stuck on the reflector body. These points were measured in ambient and then subsequently inside the climatic chamber at different temperature gradients. The difference in the coordinates of two sets of measurements provides the measure for distortion.
Case study 1
Aim: Before measurements on the actual reflector were conducted, an experiment was carried out on a flat bed (i.e., a CMM bed). The measurement was carried out on a set of retroreflective targets stuck on the specimen’s surface (i.e., the CMM bed) by using two independent measurement techniques (i.e., CRP and the CMM). Initial 3D data of these points were computed using CRP, and then further CMM measurement was carried on the same x and y coordinates of the targets. The results thus obtained were compared to check the z coordinate deviations.

Figure 2: Measurement set for CRP
Test setup
To obtain a common coordinate system that can be measured by both CRP and CMM, a magnetic V-block was kept on the surface plate (as seen in figure 2). Over the edges of the V-block, spherically mounted retroreflectors (SMR) were stuck using an adhesive that provides a bond strong enough to handle the retroreflective spherical balls (SBR) as well as the impact force that comes during replacement of SBRs by CMM-compatible spherical balls, in addition to the impact force which comes during probing by the CMM.
A total of six such SBR and SMR assemblies were used to generate a coordinate system.
111 points were stuck on the surface plate (as seen in figure 3). The tip of the CMM stylus was a sphere made of artificial ruby with a diameter of 3 mm. The CRP target was probed, and the CMM stylus made a plane with three points. In addition, a normal to the plane was found so as to go to the exact x, y, and z locations as prescribed by CRP. This further reduced the error due to pre-travel variation.

Figure 3: CMM measurement setup
Results and conclusion
1. Tooling ball measurement comparison by the two techniques:
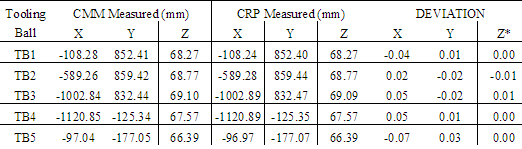
*z coordinate is the out-of-plane coordinate axis.
2. The transformation of the coordinate systems made with the help of tooling balls gave an RMS of residuals as 32 microns. It gives the best fit of the two coordinate systems (as seen in figure 4).
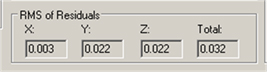
Figure 4: Best fit of the coordinate systems
3. Further, the flatness of the CMM bed was computed by both the techniques. The determinant for comparison was the RMS of the two planes:
• CMM = 0.025 mm
• CRP = 0.032 mm
The point-to-point comparison shows that variation for z deviation lies in the range of 14 microns to 83 microns, which gives a very close match between CRP and CMM measurements (as seen in figure 5).
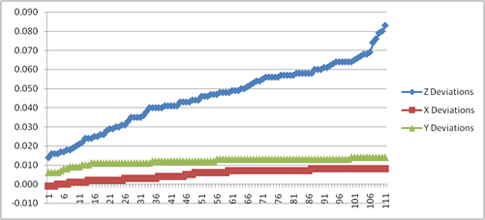
Figure 5: Point-to-point comparison of the 111 points measured by the two techniques, sorted in smallest to highest values.
4. Statistical analysis of the measured data reveals the spread of the data:

Case study 2
Aim: A similar exercise as explained in the first case study was undertaken, with the only difference being that the new test setup was to measure a 0.9 m parabolic antenna (as seen in figure 6).
The objective of this study was to establish the correlation and nearness of the measurements taken up by two different techniques via CRP and the CMM on a curved surface.

Figure 6: CRP measurement setup for 0.9 m parabolic dish
Test setup
Approximately 400 retroreflective targets were stuck on the antenna surface. These were subsequently measured by CRP. A total of six SBR and SMR assemblies were stuck on the periphery of the antenna. A common coordinate system was established using SBR and SMR. The tip of the CMM stylus was a sphere made of artificial ruby with a diameter of 3 mm. The CRP target was probed, and the CMM stylus made a plane with three points. In addition, a normal to the plane was found so as to go to the exact x, y, and z locations as prescribed by CRP.
Figure 7: 0.9 m antenna reference frame (Image from V-Stars software, Geodetic Systems Inc., www.geodetic.com.)
Results and conclusion
1. Tooling ball measurement comparison by the two techniques:
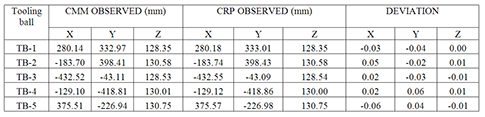
2. The transformation of the coordinate systems made with the help of tooling balls gave an RMS of residuals as 27 microns. It gives the best fit of the two coordinate systems (as seen in figure 8)
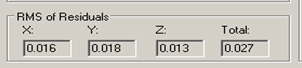
Figure 8: Best fit of the coordinate systems
3. The point-to-point comparison shows that variation for z deviation lies in the range of –245 microns to +203 microns, which gives a very close match between CRP and CMM measurements (as seen in figure 9).
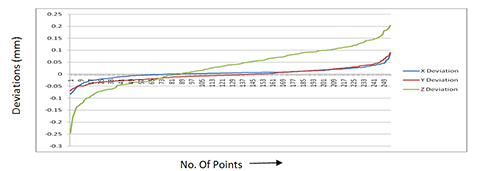
Figure 9: Point-to-point comparison measured by the two techniques, sorted in smallest to highest values.
![]()
4. Statistical analysis of the measured data to see the spread of the data:

Case study 3
Aim: After building confidence by measuring a flat bed and then a parabolic dish, the final measurement was done on a shaped reflector to ascertain the correlation between measurement by CMM and CRP techniques. The outcome of this experiment will have a major effect on the reflector’s design. If the values measured by the CMM and CRP show a close match, then the requirement of measuring the reflector inside a thermo vac chamber can be fulfilled by CRP alone as the equivalence of the point cloud measurement is established.
Test setup
Approximately 1,500 retroreflective targets were stuck on the reflector (as seen in figure 11). Scale bar and auto bars were kept to appropriately scale the measurements. To generate a common coordinate system, six tooling balls were stuck using an adhesive all through the periphery of the reflector. These tooling balls had an interface to suit both the CMM spherical balls and CRP-compatible, retro spherical balls with the same offset.
The first measurement was done using the CMM (as seen in figure 10). A coordinate system was established using the tooling balls.
Subsequently, the tooling balls data were used as nominal data by the CRP software. CRP measurement was then completed and the transformation using the tooling balls was done to arrive at the same coordinate system as that of the CMM. These data were then given to the CMM, which used the x and y coordinates as input to probe the z coordinates for all the 1,500 points.
It took six to eight hours for the CMM to measure the points, whereas it took only 1 hour by CRP (including processing) to give the coordinate values. This is an important aspect to be considered when measurements inside a thermo vac chamber are to be done. Even if it would have been possible to make measurements using a CMM inside the chamber, it would have taken almost six times longer to finish just one set of measurements.

Figure 10: Shaped reflector ready for CMM measurement (reference establishment)

Figure 11: CRP setup of shaped reflector measurement
Results and conclusion
1. Tooling ball measurement comparison by the two techniques:
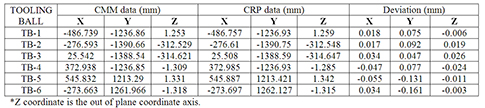
2. The transformation of the coordinate systems made with the help of tooling balls gave an RMS of residuals as 32 microns. It gives the best fit of the two coordinate systems (as seen in figure 12).
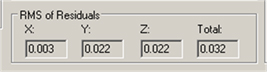
Figure 12: Best fit of the coordinate systems
3. The point-to-point comparison (as seen in figure 13) was as follows:
For x deviation: The point-to-point comparison shows that variation for x deviation lies in the range of –3 microns to +63 microns, which gives a very close match between CRP and CMM measurements
For y deviation: The point-to-point comparison shows that variation for y deviation lies in the range of –29 microns to +39 microns, which again gives a very close match between CRP and CMM measurements and is within the transformation values.
For z deviation: The point-to-point comparison shows that variation for z deviation lies in the range of –114 microns to +31 microns, which again gives a very close match between CRP and CMM measurements and is within the transformation values.
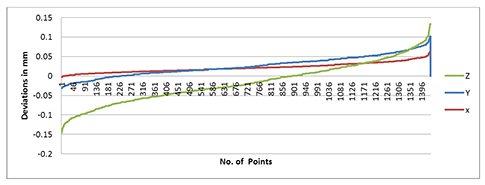
Figure 13: Point-to-point comparison on reflector measured by the two techniques, sorted in smallest to highest values
Statistical analysis of the spread of the data for z deviations:

Conclusion
This work summarizes a solution to a problem wherein it was necessary to probe common points being measured both by the CMM and CRP.
A total of three different measurement setups were prepared to compare the point-to-point accuracies on a freeform surfaces using the CMM and CRP. The first was the CMM bed, where approximately 100 targets were stuck and a common coordinate system established. The bed’s flatness was then computed using both techniques. In the second test, a 0.9 m antenna was measured by sticking 300 targets on the reflector surface. With the help of a common coordinate system, a point-to-point comparison was made to check for the maximum deviations. The final test measured a 2.2 x 2.4 m reflector where 1,500 retroreflective targets were placed and measured by CRP and subsequently by CMM in a common coordinates system. The system which was developed with the help of tooling balls. The initial aim of proving equivalence by comparing the point-cloud data was therefore met for a shaped reflector.
References
[1] Michael Wiktowy et.al. “Photogrammetric Distortion Measurements of Antennas in a Thermal-Vacuum Environment,” Canadian Aeronautics and Space Journal, pp. 65–71 , vol. 49, No. 2, June 2003.
[2] Richard S. Pappa. “Close-Range Photogrammetry & Next Generation Spacecraft,” Professional Surveyor, June 2002.
[3] A.V. Apte, R.R. Patel, Y.H. Trived. “Mechanical engineering aspects in S/c antenna alignment, measurement, and antennae-pointing requirements,” Malviya conference, India, 2002.
[4] C. Koteshwar Rao et al.“Close Range Photogrammetry: A Tool for Shape Measurement & Reflector Alignment,” Proceedings of Coordinate Metrology System Conference (CMSC) 2010, Reno, Nevada, U.S.
Add new comment