Some authors recommend that you have to wait until you have the range chart “in control” before you can compute the limits for the average chart or the X chart. Why this is not true will be the subject of this column.

To illustrate the issues we will once again use the NB10 data. The 100 values are given in the table below.

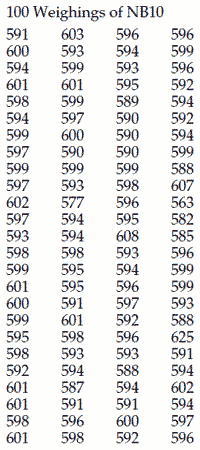
These data are the values obtained during the weekly weighings of standard NB10 at the National Bureau of Standards during 1963 and 1964. The values express the weights as the number of micrograms in excess of 9.999000 grams. Figure 1 shows the XmR chart for these data with three sets of limits.

The widest set of limits is based on the average moving range of 5.73. Dividing by 1.128 gives a Sigma(X) value of 5.08, and limits that are 15.2 units on either side of the average. With these limits we can identify three occasions when there were problems with weighing this standard.

 …