Story update 6/18/2012: A couple of confusing references to Taguchi methods were removed.
During new product development, computational fluid dynamics (CFD) is often used in the design stage to simulate such things as the effect of air flow on cooling. The problem with CFD is that it can take a long time to find the solution due to the number of iterations that must be performed.
|
ADVERTISEMENT |
Since the architecture of the CFD software is based on solving the field equations, the time needed to complete a CFD run depends on the degree of convergence, or accuracy, expected. Long run times can tremendously increase the cost and the turnaround time of a project, an important aspect to consider when you are in a war to beat the competition.
An alternative to using CFD alone is to cut down on the number of iterations by using design-of-experiments (DOE) to preselect runs that you know are going to yield results close to what you are looking for. This reduces simulation bottlenecks, thus increasing productivity and efficiency while maintaining the required accuracy levels. The number of runs can be further refined and optimized using the Monte Carlo approach.
One such study and comparison between CFD analysis and the statistical techniques mentioned above is demonstrated below. In this example, I explain how using DOE reduces the number of runs using some optimum combinations. These combinations will then be run through the CFD software to get the results. Monte Carlo further optimizes the runs which again must be run using the same CFD software to get the refined optimized results to the required accuracy or convergence levels.
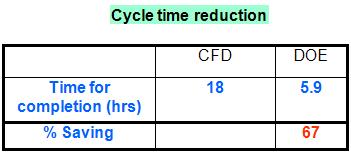
In effect, standalone CFD has taken 23 iterations and 18 hrs, where as optimization using a combination of DOE and Monte Carlo has taken eight iterations and 5.9 hrs.
CFD approach using standard commercial dedicated software
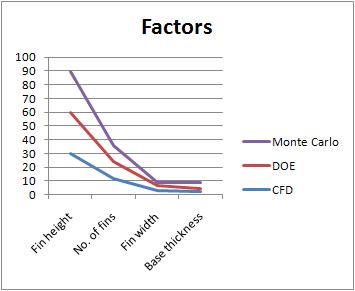
In this example thermal analysis was carried out for a printed circuit board (PCB), including the heat sink and a fan, which was used as a forced convection source. Fin height, number of fins, fin width, and base thickness were the factors considered for the given heat sink. The details of PCB and IC chip were also considered in the analysis.
The fan flow characteristics were then measured, and a fan with a particular flow characteristic was selected for the analysis. The analysis phase involved using a specific software for the CFD analysis in the order detailed below:
• The given problem was modeled using software that was specially suited for CFD analysis.
• The requisite boundary conditions were assigned and the analysis was carried out.
The integral optimization module within the software optimized the junction temperature by varying the factors mentioned above within their assigned lower and upper bound limits.
The complete optimization run took 23 iterations and 18 hours.
Finally, a prototype with a similar configuration was made, and the actual junction temperature was measured and found to be within the acceptable limits.
Using Minitab for DOE
In this alternate method, we used Minitab’s DOE features to reduce the number of iterations required for our CFD.
Step 1: Select four factors and assign two levels each, one high and the other low. Assuming uncoded levels, the number of runs generated by Minitab for half factorial design is as follows:
|
Experiments |
Heat sink base thickness |
Fin height |
Fin thickness |
Number of fins |
|
Run 1 |
-1 |
1 |
1 |
-1 |
|
Run 2 |
-1 |
-1 |
-1 |
-1 |
|
Run 3 |
1 |
-1 |
1 |
-1 |
|
Run 4 |
-1 |
-1 |
1 |
1 |
|
Run 5 |
1 |
-1 |
-1 |
1 |
|
Run 6 |
-1 |
1 |
-1 |
1 |
|
Run 7 |
1 |
1 |
-1 |
-1 |
|
Run 8 |
1 |
1 |
1 |
1 |
Step 2: Carry out the runs in the CFD software and tabulate the results.
Step 3: Study the Main effects and Interaction plots.
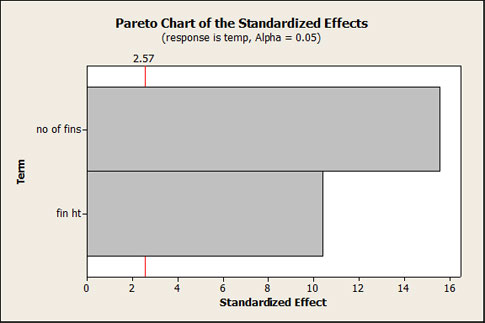
Step 4: Analyze the Pareto plot to estimate the contribution of each of the factors toward the end result.

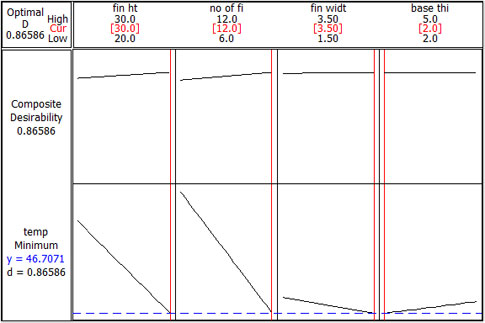
Step 5: Refine the analysis further to eliminate the uninfluential factors, and then study the effects of the two main contributing factors (i.e., fin height and number of fins).

The complete optimization took eight iterations and 5.9 hours.
If you carry out another CFD iteration with the levels as suggested by DOE for the above-mentioned factors, the results will be within 2-percent deviation with respect to the optimized CFD results. This is carried out mainly to fine-tune the model.
Monte Carlo approach using Crystal Ball software
To further refine the number of runs required in CFD, we used a Monte Carlo approach.
Step 1: Define the assumptions by way of distributions for all four factors under study, along with the minimum and the maximum values.
Step 2: The forecasting factors are the transfer function or the regression equation generated out of the DOE runs, both for the four factors and the optimized two factors.
Step 3: The sensitivity analysis of the data reveals the same factors as suggested by DOE. The correlation and overlay plots are in sync as shown below.
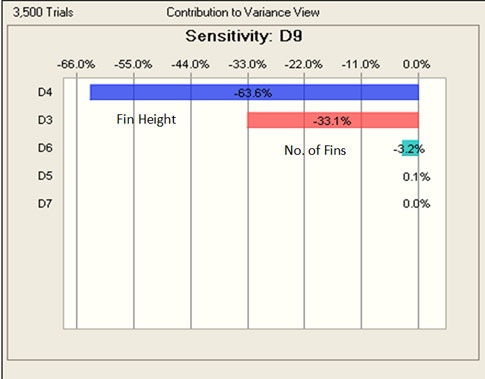
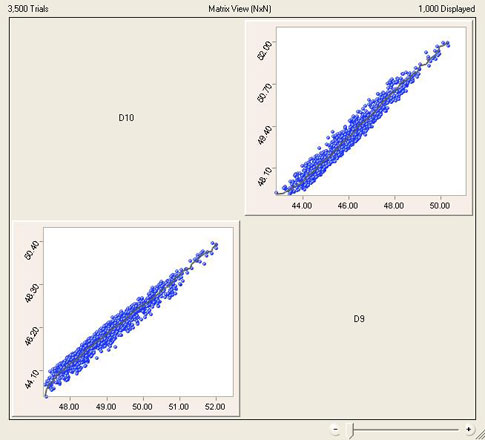
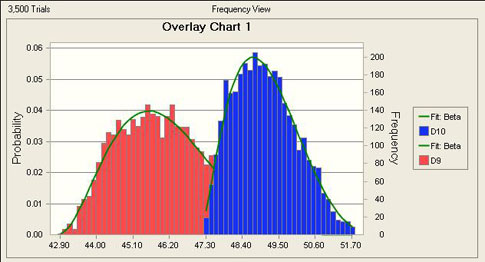
Step 4: Refine the model further by using the levels of the factors as suggested by the Monte Carlo iterations, and run an additional iteration in CFD. The optimized result of junction temperature will be much closer to the original value that was obtained from the former CFD analysis without using DOE.

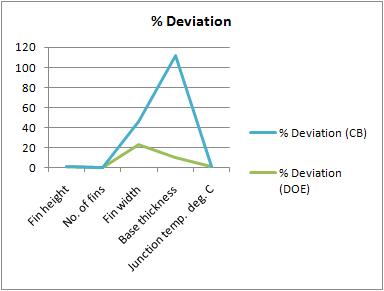
Step 5: Study the percentage deviation of the various factors with respect to the DOE and Monte Carlo analysis. The values of the significant factors are in line with the DOE results.
Conclusion
|
DOE approach |
Monte Carlo approach |
|
DOE gives the optimum levels for the experiments. |
In Monte Carlo the levels can be interpolated further for fine tuning. |
|
DOE gives the transfer function. |
In Monte Carlo the transfer function can further be used for forecast analysis. |
|
DOE gives the main effect plots. |
Monte Carlo gives the sensitivity analysis. |
|
DOE gives the interaction plots. |
Monte Carlo gives the forecast plots. |
This case study shows that combining DOE along with Monte Carlo analysis is a good tool for cycle time reductions in areas involving repeated iterations. Optimizing the rest of the factors is open for discussion. This gives rise to the scope for further optimization based on cost, weight, and other parameters.
Comments
DOE to the Rescue article
Nice example combining simulation with factorial (one-half fractional) DOE. Just one small point, though. The array format was conventional factorial DOE, not Taguchi's. Also, a question: was variation relative to the mean considered (e.g., with the signal-to-noise ratio from Dr. Taguchi that considers this)? A very good study, but perhaps there might have been some effectiveness improvement with use of Parameter Design and a follow-up DOE on the preferred levels of the more critical control factors. These comments aren't intended to be critical, just some points and suggestions.
DoE
Agree with Mike - i did not see application of Taguchi's arrays or S/N ratio analysis in this article . A good article nevertheless
DOE to the Rescue
Add new comment