With SPC work, we normally try to analyze a process distributionís shape, central tendency and spread. We usually measure this last item by computing an estimate of the process standard deviation, or sigma, designated with the Greek letter s. There are several ways to do this; Iíll discuss the pros and cons of some of the more common methods used to estimate s. Weíll refer to these s estimates with the symbol s. For the purpose of discussion, I invented a data set to analyze, as shown in Table 1. The data reflects a process that starts with an average of 10. The process is influenced by a special cause that makes the average increase by 1 every hour. The standard deviation remains constant at 1, and the data follow a normal distribution. Method No. 1: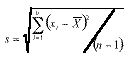 This is the standard approach, used by calculators and spreadsheets any time users require sample sigma. The numerator is the sum of the squared deviations from the sample average -- i.e., subtract the sample average from the first observation and square it, then the second, etc. Then add the results. If the data cluster close to the average, this sum will be smaller than if they are scattered more widely. Thus, a bigger value of s indicates a process with greater scatter. The denominator indicates the degrees of freedom. The n - 1 term in the denominator is a bias correction. For a given sample size, the denominator will be a constant. Thus, estimates of s can be compared directly for different processes when sample sizes are the same. Any observed differences can be attributed to data scatter, which may (or may not) indicate different process scatter. Shewhart showed that this traditional estimate of s is only valid when the process is stable. If a process is influenced by a special cause, then this estimate will overestimate the process scatter. For our example, the formula estimates s as 3.337, far greater than the actual value of 1. The difference is due to the trend created by the special cause. Because the estimate includes variation from the special cause, detecting the special cause is harder to do. The 3-sigma limits from this estimate are 4.446 and 24.468, which include all of the data. Method No. 2: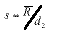 Using an estimator that doesnít include the variation between time periods will alleviate the problem of s being inflated by special causes. Shewhart proposed using rational subgroups to do this. A rational subgroup is a sample selected in such a manner that the opportunity for a special cause to influence the results is minimized. This is often accomplished by selecting consecutive units from a process. In Table 1, the data are arranged in 10 subgroups of five measurements per subgroup. The first group of five were sampled in hour No. 1, the next group in hour No. 2 and so forth. The table indicates no change in the process during the time the subgroup was collected, so itís the ideal from the Shewhart perspective. With these ďcleanĒ subgroups, we can estimate the process dispersion for each subgroup, then combine the results to find the overall estimate of s. One way to estimate dispersion is to find the range, R, by subtracting the smallest observation in the subgroup from the largest. After doing this, we can average the R values and use a correction factor, d2, to find s. For subgroups of 5, the d2 factor is 2.326; for our data, the average range is 2.665. This gives s = 1.146, which is much closer to 1.0. Method No. 3: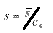 The range uses only two data values from each subgroup, which poses a problem. In statistical terms, itís inefficient. That is, the estimates of s based on the range will be more erratic than when subgroup s values are used. The range estimate inefficiency gets worse as the subgroup size increases. Method 3 works by finding the subgroup s values, then averaging them to get s and dividing this by the bias-correction factor c4. Subgroup s values are computed using the formula shown in method 1 for each subgroup separately. Obviously, this is more tedious than finding the range for each subgroup. With method 3, we get an estimate of s = 1.158 for our data. Method No. 4: s=1.047Moving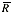 If it isnít possible or desirable to collect data in subgroups, we can correct for special causes by finding the range between consecutive hourly samples. To get s, we must multiply the median moving range, 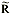 , by the correction factor 1.047. For our data, we get s = 1.654. The estimate is somewhat larger than the estimates we obtained from subgrouped data because the moving ranges donít completely factor out the differences between the subgroup. However, the estimate is closer to the correct value than the s value found with method No. 1. Recent research suggests that this approach gives good results for a wide variety of out-of-control patterns. , by the correction factor 1.047. For our data, we get s = 1.654. The estimate is somewhat larger than the estimates we obtained from subgrouped data because the moving ranges donít completely factor out the differences between the subgroup. However, the estimate is closer to the correct value than the s value found with method No. 1. Recent research suggests that this approach gives good results for a wide variety of out-of-control patterns. Method No. 5: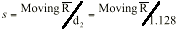 This method for estimating s is based on the average moving range, 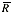 . Doing this for the sample data set gives s = 1.532. Because itís also based on the moving range, this estimate suffers from the same shortcomings as method No. 4. . Doing this for the sample data set gives s = 1.532. Because itís also based on the moving range, this estimate suffers from the same shortcomings as method No. 4. Table 2 summarizes the results of all of these methods. The least accurate result is found when the standard formula is used. For SPC work, this formula should only be used when a control chart shows good statistical control. Despite the fact that, for our example, the 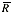 result was slightly more accurate than the result was slightly more accurate than the 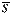 estimate, the best formula from a statistical perspective is method No. 3. For subgroups of five, the advantage isnít all that great, but it becomes greater as the subgroup size increases. The estimate, the best formula from a statistical perspective is method No. 3. For subgroups of five, the advantage isnít all that great, but it becomes greater as the subgroup size increases. The 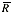 method usually comes in second to the method usually comes in second to the 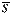 method, unless the statistical advantage is outweighed by some practical concern -- such as ease of understanding. method, unless the statistical advantage is outweighed by some practical concern -- such as ease of understanding. The moving range methods, while inferior to the subgroup methods, are far better than the standard s formula. Generally speaking, the median moving range estimate gets the nod over the average moving range estimate. About the author Thomas Pyzdek is president and CEO of Quality Publishing. He has written hundreds of articles and papers on quality topics and has authored 13 books, including The Complete Guide to the CQM and its accompanying CD-ROM. Comments can be e-mailed to Tom Pyzdek. |

