Last month we met Hartford Simsack, Greer Grate and Gate's (GG&G's) quality manager with connections. (His
brother-in-law had hired him, after he emerged from a short prison term, in spite of his paucity of qualifications.) When Franklin Benjamin, a technician, challenged him with a statistical
problem, Simsack was able to retain his veil of competence by soliciting the opinion of his statistics professor at the community college where he had enrolled in an effort to learn something
about SPC. Things are not going particularly well with his statistical education, but Simsack has learned that by continuing to enroll in courses, he will retain the resource
that he has found in his professor, Dr. Stan Deviation. Simsack is one of those students who are not especially motivated by grades. After all, his current position demands only that he keep his
head above water and have the appearance of being knowledgeable about SPC. He feels certain that his knowledge has impressed technician Benjamin. Benjamin, on the other hand,
felt empowered by the answer to his question about a series of points below the mean. He had suspected the correct answer, and Professor Deviation's solution--imparted through Simsack--simply
verified it. Benjamin has begun to wonder why he can't be quality manager, because he obviously knows so much. The first challenge to his new-found self-assurance has come in
the form of--you guessed it--a capability question. And that means dealing with suppliers. His world is expanding. A GG&G supplier, Rhott Iern Production, has been
challenged to provide evidence of process capability. The supplier's quality manager, Ms. X. Trusion, insists that the process is indeed capable. (Her first response when her supervisor asked
whether the process was capable had been "of doing what?" She has since polished her statistical language and now knows that process capability is a measure of whether a process is capable of
meeting established customer specifications or requirements.) X. Trusion and her team are determined to investigate the Cpk of the process for which they are responsible. Of
course, the first and most critical requirement for a capability study is knowledge that the process is stable. A further demand is that it be normal. A mistake commonly made in beginning
capability analysis is forgetting that both conditions must exist before a capability analysis can be considered valid. The process must be stable (in control) as reflected in a control chart,
and the data that it generates must reflect a normal distribution. "Everyone knows that," Benjamin pointed out. X. Trusion made a mental note to refer to her textbook to learn more about
stability and normalcy. Benjamin went on, reciting nearly verbatim what Simsack had told him: "The chi-square test is one of the ways to determine whether a process is normal."
X. Trusion is dejected by this news, for she believes that the test to which Benjamin is referring is a fraternity initiation rite that she knows nothing about. Benjamin has often boasted
loudly about his days as a college Greek, and she assumes that this is another way to make her feel left out. After all, on Benjamin's campus, being a member of a fraternity was the normal way to
go. What can you tell X. Trusion about the chi-square test, not only to restore her self-esteem, but to provide a useful tool for evaluating normalcy of a process?
Answer: Determining that a distribution is normal can be tricky. One method is the chi-square
technique. Figure 1 illustrates a normal distribution. The red vertical lines between the histogram cells and the normal curve indicate the difference between the actual data set and the normal
distribution. The data do indeed follow a normal distribution. Figure 1: A Normal Distribution
Figure 2: A Bimodal Distribution
The chi-square statistic calculates the actual difference between the data and the normal distribution. In the example, there is only a small shaded area; this would
produce a small chi-square value. In Figure 2, a much larger difference exists between the theoretical normal and the
actual data. The data demonstrates a bimodal distribution. The chi-square value would be large in this case, so it does not reflect a normal distribution. The
chi-square value is calculated with this formula: 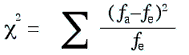
ƒa = actual frequency per cell ƒe = expected frequency per cell The actual calculation of c2
is not complex, but it is somewhat unwieldy. Software is available to aid in these calculations. About the author Michael J. Cleary, Ph.D., is founder and president of PQ Systems Inc. E-mail him at mcleary@qualitydigest.com |