Digging Into DOE
Selecting the right central composite design for response surface methodology applications _________________
by Richard Verseput
Research and
development are the heart and soul of improvement efforts in manufacturing, and it's fast becoming standard practice to employ design of experiments methods in industrial R&D. In the early
stages of their work, experimenters typically use screening experiment designs that normally consist of trials run at the extreme lower- and upper-bound level setting combinations of the variable
study ranges. They provide information on the direct additive effects of the study variables and on pairwise (two-variable) interaction effects. Screening designs enable experimenters to select
the best materials and equipment from available alternatives and to focus on the correct variables and ranges for further study. In the later stages of the experimental work,
the goal shifts from screening to product and process optimization. The statistical experiment designs most widely used in optimization experiments are termed "response surface designs." In
addition to trials at the extreme level settings of the variables, response surface designs contain trials in which one or more of the variables is set at the midpoint of the study range (other
levels in the interior of the range may also be represented). Thus, these designs provide information on direct effects, pairwise interaction effects and curvilinear variable effects. Response
surface methodology, one approach to product and process optimization work, derives its name from the use of these widely used optimization experiment designs. Most
practitioners of RSM now generate their experiment designs and analyze their data using a statistical software program running on a personal computer. Many of these software programs can generate
many classes of RSM designs and, in some cases, offer several varieties of each class. However, the central composite design is the most popular of the many classes of RSM designs due to the
following three properties:  A CCD can be run sequentially. It can be naturally partitioned into two subsets
of points; the first subset estimates linear and two-factor interaction effects while the second subset estimates curvature effects. The second subset need not be run
when analysis of the data from the first subset points indicates the absence of significant curvature effects. A CCD can be run sequentially. It can be naturally partitioned into two subsets
of points; the first subset estimates linear and two-factor interaction effects while the second subset estimates curvature effects. The second subset need not be run
when analysis of the data from the first subset points indicates the absence of significant curvature effects.
 CCDs are very efficient, providing much information on experiment variable
effects and overall experimental error in a minimum number of required runs. CCDs are very efficient, providing much information on experiment variable
effects and overall experimental error in a minimum number of required runs.
 CCDs are very flexible. The availability of several varieties of CCDs enables their use under different experimental regions of interest and operability. CCDs are very flexible. The availability of several varieties of CCDs enables their use under different experimental regions of interest and operability.
Three main varieties of CCD are available in most statistical software programs:
face-centered, rotatable and inscribed. Many experimenters are uncertain about the best variety to use in a given study. To make the right selection, the experimenter
must first understand the differences between these varieties in terms of the experimental region of interest and region of operability, according to the following definitions.  Region of interest
--a geometric region defined by lower and upper limits on study-variable level setting combinations that are of interest to the experimenter Region of interest
--a geometric region defined by lower and upper limits on study-variable level setting combinations that are of interest to the experimenter
 Region of operability --a geometric region defined by lower and upper limits on
study-variable level setting combinations that can be operationally achieved with acceptable safety and that will output a testable product Region of operability --a geometric region defined by lower and upper limits on
study-variable level setting combinations that can be operationally achieved with acceptable safety and that will output a testable product
The face-centered CCD
Figure 1: Two-Variable Face-Centered CCD
|
Figure 1 presents a face-centered CCD for two study variables: time and temperature. Both coded and natural variable level settings for time and temperature are shown in the
figure. The design consists of a center point, four factorial points (the intersection points of the ±1 coded variable bounds) and four axial points (points parallel to
each variable axis on a circle of radius equal to 1.0 and origin at the center point). The dots in Figure 1 identify the variable level setting combinations that constitute the nine design points
(experiment runs).
Note that the radius, designated a, determines the geometry of the design region. An a
of 1.0 defines a square design geometry (a cube for three variables, a hypercube for four or more variables, etc.). As the value of a increases, the axial
points extend beyond the faces of the square and the design region becomes more spherical. To successfully carry out any designed experiment, the region of operability must
encompass the region of interest. In this example, this means that the process must be able to be operated at all time and temperature level setting combinations in the
region of interest described by the variable ranges. Therefore, the first step in selecting the right variety of CCD is to compare the region of interest to the region
of operability. If the process can't be operated at one or more of the extremes of the region (in this case the corners of the square), then a face-centered CCD is
inappropriate. This leaves the experimenter with two options: reduce the variable ranges and generate a new face-centered CCD, or generate an inscribed CCD. The
process for making this decision will be discussed in the section on inscribed designs.
Figure 2: Two-Variable Rotatable CCD
|
The rotatable CCD Figure 2 presents a rotatable CCD for time and temperature using the previously defined
lower and upper variable bounds. As the figure shows, the rotatable CCD uses an a value of 1.4 to describe a circular design geometry (a sphere for three
variables, a hypersphere for four or more variables, etc.). You may recognize this design as the one used in Example 14-2 of Design and Analysis of Experiments by Montgomery.1 For a given number of variables, the a value required to achieve rotatability is computed as a = 4
¥&F where F is the number of points in the 2k factorial design (k is the number of study variables). Rotatability refers to the uniformity of prediction
error. In rotatable designs, all points at the same radial distance (r) from the center point have the same magnitude of prediction error. Note that in most rotatable
designs the factorial points and axial points lie on different concentric geometric spheres and thus have different magnitudes of prediction error. For example, in the 23
rotatable CCD, the factorial points are located on a sphere of radius 1.73, while the axial points are located on a sphere of radius 1.68. Setting the a
to ¥k changes the design from a rotatable CCD to a spherical CCD. In spherical CCDs, all design points occur on the same geometric sphere. These
designs are not exactly rotatable, but they are near-rotatable. As stated in Myers and Montgomery,2 "If the desired region of the design is spherical, the CCD that is
most effective from a variance point of view is to use a = ¥k and three to five
center runs." Generally a spherical design region is desired when the experimenter strongly suspects that the response will express a simple maxima or minima within
the study variable ranges. As previously stated, it's required when the process can't be operated at one or more of the extremes of the design region.
The value of making rotatability (or near-rotatability) a design goal becomes clear when you consider that the experimenter doesn't know the location of the optimum
point within the region of interest before the experiment is conducted, so it's desirable that all points a given distance (r) from the center point in any direction
have the same magnitude of prediction error. Relative to the a value of 1.0 in the face-centered design, the rotatable design a
value of 1.4 has extended the design region beyond the defined variable bounds. Thus, predicted responses at or near the axial points, which would have been
extrapolations in a face-centered design, are now within the design region. This is an important consequence, because the magnitude of prediction error increases
geometrically with distance outside the design region. However, extending the axial points beyond the defined variable bounds when
using rotatable CCDs requires operating the process at five level settings of each variable (as will be shown later, the same is true of inscribed CCDs). The
face-centered CCD, in contrast, requires operating the process at only three level settings of each variable. This makes the face-centered CCD a simpler design to carry out.
As previously stated, a face-centered CCD can be used when the region of operability encompasses the region of interest as defined by the variable bounds. To
decide between a face-centered CCD and a rotatable (or spherical) CCD in this case, the experimenter must decide whether the rotatable design benefits of uniform
prediction error and extension of the design region adequately offset the added complexity of operating the process at two additional level settings of each variable.
The experimenter should not take this added complexity lightly. Even when reconfiguring the process is not expensive and time-consuming --and it's normally
both --the increased number of reconfigurations provides a much greater opportunity for sources of experimental error associated with setup and operation
to express themselves. It's my experience that unexpectedly large experimental error is the most common cause of failure in studies employing designed
experiments, and it makes sense to select options that reduce the chance of error expression. For the following two reasons, the benefits of rotatable designs do not
offset the added complexity and associated risk in most cases, making the face-centered CCD more than adequate for most experiments. Reason 1: Insufficient reduction in prediction error
Table 1: Axial Point Prediction Errors--Two Variable CCDs
|
|
Given a reasonable overall experimental error, rotatable designs do not greatly reduce prediction error at the rotatable design axial points. Table 1 presents the
axial point 95-percent prediction intervals for two-variable and three-variable rotatable and face-centered CCDs. The first two rows of the table use the model
prediction error variance (MSE) from Example 14-2 of Design and Analysis of Experiments by Montgomery for the yield
response. The last two rows of the table use an MSE of 16 based on a 5-percent relative error and a maximum yield result of 80 percent.
For the Montgomery data, the 95-percent PI for the axial points is ±0.802 (recall that the axial points are design points in the rotatable CCD). For a face-centered
CCD, predictions at the axial points would be extrapolations. However, the 95-percent PI for the axial points is ±0.991 for the face-centered CCD. In practical
terms, a reduction from ±1.0 to ±0.8 in the 95-percent P.I. for a predicted yield of, say, 80 percent is of no real consequence. The same lack of practical consequence
is true for reduction from ±14.9 to ±12.1 given a 5-percent RSD. For the k = 3 designs, the reductions in the 95-percent PI seem more
consequential. However, one must remember that the rotation a value increases from 1.4 in the k = 2 CCD to 1.68 in the k = 3 CCD. This means that the
experimental ranges have been extended by 1.68 times the original ranges defined by the experimenter, for example from 10 minutes to 16.8 minutes for time. Reason 2: Insufficient difference in effects estimationTable 2: Regression model Coefficient Data--Exanmple 14-2 From Montgomery
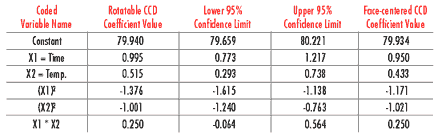 |
Table 2 presents the estimated regression model coefficients and corresponding
±95-percent confidence intervals from Example 14-2 of Design and Analysis of Experiments by Montgomery for the yield response. The last column in the table
presents the estimated coefficients using a 13-point face-centered CCD for the same variables. The actual yield data from Example 14-2 were used for the center
points and factorial design points that the two designs have in common. Predicted yield data were used for the face-centered axial design points. The predictions were
obtained using the regression model from Example 14-2 with a correctly propagated experimental error added to each predicted value. As the Table 2 data show, the
face-centered CCD coefficients are all within the rotatable CCD coefficient ±95-percent confidence intervals. In fact, a comparison of the estimated
coefficients for the two design types clearly shows that they are either identical or nearly so in all cases.
The inscribed CCD
Figure 3: Two-Variable Inscribed CCD
|
|
Figure 3 presents an inscribed CCD for time and temperature, again using the previously defined lower and upper variable bounds. The inscribed CCD also uses an a
value of 1.4 to describe a circular geometric region (a sphere for three variables, a hypersphere for four or more variables, etc.). However, inscribing restricts the actual design region to the
defined variable ranges by locating the axial points at the lower and upper bounds of the variable ranges. The factorial points are brought into the interior of the design
space (inscribed) and set at a distance from the center point that preserves the proportional distance of the factorial points
to the axial points. For example, given a rotatable CCD for two variables (a = 1.4) with coded variable bounds of ±1, the factorial points would range between -1 and
+1 and the axial points would range between -1.4 and +1.4. In the corresponding inscribed design, the factorial points would range between -0.7 and +0.7 and the
axial points would range between -1 and +1. The inscribed option is a convenient way to generate a rotatable CCD that enables
the experimenter to study the full ranges of the experiment variables while excluding nonallowable operating conditions at one or more of the extremes of the design
region. The excluded portion of the original face-centered CCD region is shown in gray in Figure 3, as are the excluded face-centered CCD points. However, for the k
= 3 inscribed CCD, the 95-percent PI for the eight excluded factorial points is ±1.074, as opposed to ±0.788 for the face-centered CCD that
contains these points. This means that the prediction error will be 36-percent higher (1.074/0.788) for the extreme points that are excluded by the inscribing but are
within the region of operability of the face-centered CCD. When only one extreme point is nonallowable, eliminating that run from a face-centered CCC only increases
the prediction error for four design points --by 7.4 percent for three axial points and by 10.8 percent for one extreme point. It's better in this case to generate a
face-centered CCD and simply not run the nonallowable point rather than suffer a 36-percent increase in prediction error for the seven extreme points excluded by
inscribing but within the region of operability. General guidelines for CCD selection
A rotatable or near-rotatable CCD should be used when nonallowable operating conditions exist at two or more of the extremes of the design region. The inscribed
design may be the best rotatable design option in this circumstance, because experimenters commonly think of setting individual variable bounds in terms of
practical or operational limits. The inscribed design lets the experimenter define the variable bounds in these terms while excluding nonallowable operating conditions at
the extremes of the design region. A face-centered CCD, on the other hand, should be used whenever the region of
operability encompasses the full region of interest as described by the variable ranges or when nonallowable operating conditions exist at only one of the extremes of the design region. In rotatable and near-rotatable CCDs, each experiment variable is represented at five levels. The face-centered CCD requires only three levels of each experiment
variable, making it the simplest variety of CCD to carry out as well as the least prone to corruption due to sources of experimental error associated with setup and operation.
Compared to face-centered CCDs, rotatable or near-rotatable CCDs offer reduced prediction error for, and improved estimation of, quadratic (curvature) effects.
However, given a reasonable magnitude of overall experimental error, say a 5-percent RSD, these benefits do not outweigh the added complexity of requiring each variable to be run at five levels.
References 1. Douglas C. Montgomery. Design and Analysis of Experiments
, 4th Edition, John Wiley and Sons. New York: 1997. 2. Raymond H. Myers and Douglas C. Montgomery. Response Surface Methodology, John Wiley and Sons. New York: 1995. About the author Richard Verseput is president of S-Matrix Corp. ( www.s-matrix-corp.com ). He has published many articles on applied DOE, and has created and taught applied
DOE courses in the aerospace, automotive, biotechnology, chemicals and pharmaceutical industries. E-mail him at rverseput@qualitydigest.com . |