|
|
|
|
Today's Specials |
|
|
|
|
SPC |
 |
|
Recognizing the Real Goal Improvement is the key. The way you get there is irrelevant. |
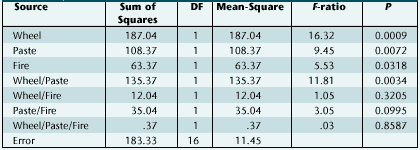
If I have one major weakness, it's that I tend to skip over the details and go directly for the prize. There is an old Chinese proverb (actually I heard it on "Kung Fu") that goes: "In every loss there is a gain. In every gain there is a loss." My motto is "Keep your eyes on the prize." I tend to be a little casual about details, but this allows me to focus on improvement instead of theory. Statistical process control (SPC) involves mathematical modeling. Basically, we make a model and compare it to the real world. Control charts are mathematical models that predict the future based on what has occurred in the past. But the real purpose of control charts is not to make the model or even to compare it to the real world; the real purpose is to become one with the process, to develop a thorough understanding of it. Too many people get hung up in tiny, specific details and fail to make any progress toward process improvement. They don't keep their eyes on the prize. Let me give you an example. What is the standard deviation of the data set 1, 2, 3, 4, 5? If you have a clever calculator, it has a key for the standard deviation, usually marked with a lowercase Greek sigma (s). If you have a very clever calculator, it will have two keys for the standard deviation. One will be a lowercase Greek sigma with a subscript of "n -1" (sn-1). The other will be a lowercase Greek sigma with a subscript of "n" (sn). The difference between these two symbols is beyond the scope of this particular column. But my point is that people call both of these calculations "standard deviation." Actually, statistics professors don't call them that, but statistics professors aren't people (just kidding). Anyway, there are two different ways to compute the standard deviation. For our data set 1, 2, 3, 4, 5, sn -1 yields 1.581 and sn gives us 1.414. The descriptive statistics option in Excel also gives 1.581. A popular SPC software package yields both numbers but calls one the "population sigma" and the other the "sample sigma." Anyone confused yet? Which one of these numbers is right? If n is large, these two statistics are almost the same. Much of statistics is just specialized vocabulary, and the more you get into statistics, the more obscure the vocabulary becomes. I have always thought of SPC as a tool to help me make process improvements. I have always considered statistics a small part of SPC. As I get further and further into the details of statistics, I get less and less interested. In part this is because I'm lazy. And in part it's because I've never found a lot of use for the more arcane areas of statistics. In July, I published a column on designed experiments. My intention was to show how they could be used as tools to make process improvements. Part of my article dealt with analysis of variance (ANOVA). The way I do ANOVA is by clicking on the ANOVA icon in my statistics program, letting everything default and watching the computer crank. Some readers tried to duplicate my analysis. I must say I admire their devotion, and I would like to apologize to those who went to all this trouble and got results different from the ones I published. It turns out that, just as there are different ways to compute the standard deviation, there are also different ways to do ANOVA. Different people set different parameters in the model to different levels. As far as the July column goes, I think that, while I was using a model without a constant term, my readers were using models with a constant. The statistical analysis programs being used allow the analysis to be done either way, and there are some advantages to doing it with a constant. I didn't make a conscious decision to do the analysis without one; that was just the computer's default setting. Table 1 shows the results some of my readers got. Table 1: Analysis of Variance
Is this way of doing ANOVA right? Is the way I did it wrong? I don't know. And to be quite frank, I don't care. The important thing is to get out on the floor, collect the data and find out why the process isn't working right. Regardless of how you do the analysis, the conclusion remains the same. The most important variable in this process was the kind of wheel used to grind the ceramic. I get valuable comments about every column I publish, and heaven knows I can use the help. But, please, keep your eyes on the prize. The goal is to make the process better. About the author Gregory P. Ferguson is quality manager of Parker Hannifin's Tucson, Arizona, facility. He has published technical articles and assisted in the publication of two books. Comments can be e-mailed to him at gferguson@qualitydigest.com . |
Menu Level Above
This Menu LeveL
Menu Level Below
Copyright 1999 QCI International. All rights reserved.
Quality Digest can be reached by phone at (530) 893-4095. E-mail: Click Here