SPC in the Boardroom?
December’s a fading memory and the data are in. It’s time for the annual review, i.e., “trending” the three-month performance of the fourth quarter and comparing those results to last year’s fourth quarter and this year’s third. From this, we can determine overall trends, percent changes, and variances from goals and/or budgets.
Did you know that, given three different numbers, there are six distinct ways they can appear? The graphs below show the possibilities, along with several very common terms used to “explain” them.
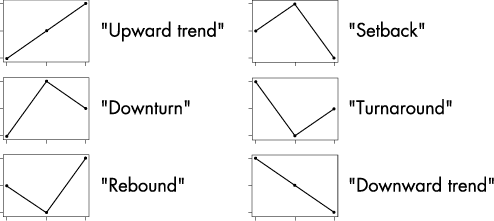
The question isn’t whether the numbers differ from one another. The deeper question should be, “Is the process that produced the third number the same as the process that produced the second and first numbers?”
I’ve developed an analog of W. Edwards Deming’s red bead experiment, where I ask a roomful of people to flip a coin, ask those who obtain heads to flip it again and count the number of people who get the “double head.” (In a future column I’ll describe that experiment in more detail as a substitute for the red bead experiment.) At the end of three such flipping sequences, we have one of the six patterns. I then use a p-chart calculation to show the expected range for double heads, given the number of participants in the room. For example, for a room of 50 people, this expected range is three to 21.
Here’s the point: As long as the three numbers we’ve obtained lie within the limits I calculate, they’re indistinguishable because the process hasn’t changed--it’s still 50 people flipping a coin twice. To calculate percent changes, attribute a trend, “explain” the sequence of three using any of the six terms, or distinguish between individuals’ performances because they obtained zero, one, two or three double heads is totally inappropriate.
Suppose I now had the same 50 people flip the coin only once, counted the number of heads, and obtained 25? (A reasonable assumption.) Notice that this is greater than the previously calculated upper limit and was produced by a different process--i.e., flipping once instead of twice.
As you can see, calling a sequence of three observations that all either increase or decrease a “trend” without a context of variation has a 33-percent risk of being random--or two out of six random possibilities.
Statistical theory tells us that in the absence of a context of variation (as is the case in most managerial meetings), it takes a sequence of six consecutive increases or decreases to declare a trend (with 20 data points or fewer, you may use five).
In my experience, this is relatively rare. Simpler statistical tests are available that will detect a change much sooner, e.g., the test described in last month’s column of eight in a row either all above or all below the median when the data are plotted as a run chart. (See January 2005 Quality Digest or visit www.qualitydigest.com.) Or, as in the case of changing the “flipping” process, the data fall outside the variation limits--assuming you even know what they are.
Which brings me to the question: Why do most monthly meetings focus only on “this month vs. last month vs. 12 months ago,” when there are 10 “in between” months?
Any sequence of numbers needs a context of variation within which to be interpreted. This variation is inherent to the process and must be calculated from process data. It’s not based on intuition or what someone “thinks” it should be, generally either an arbitrary number ending in zero or five or an arbitrary percentage (ending in zero or five) of the average. This applies to managerial data as well as production data. A process is a process.
Davis Balestracci is a member of the American Society for Quality and the Association for Quality and Participation. He previously served as chair of the statistics division of ASQ. His book, Quality Improvement: Practical Applications for Medical Group Practice (Center for Research in Ambulatory Health Care Administration, 1994), is now in its second edition. Visit his Web site at www.dbharmony.com.
|