What Is 'Small'?

Even large samples can lead you into the murky realm of hasty generalization.

Sometimes, despite our best efforts, we're faced with sample sizes that just seem too small. The problem we're trying to avoid is a logical fallacy known as "hasty generalization." According to Wikipedia, "Hasty generalization, also known as fallacy of insufficient statistics… is the logical fallacy of reaching an inductive generalization based on too little evidence." Statistically, there are two basic problems:

1. The sample isn't valid.

2. The sample isn't reliable.

Validity means that the sample measures what it's supposed to measure. If my sample is small and the population is large and varied, my sample is unlikely to represent all the richness and variety of the population.

Reliability, in a statistical sense, means consistency in the result. If repeated samples produce different results, the samples are unreliable. For example, if I survey n = 2 customers, the variation between repeated samples is likely to be so large that my conclusions would change frequently. Each sample unit is weighted equally, but when the sample is small this equal weighting overestimates the importance of any sample unit that's not close to the population mean. In other words, small samples tend to be biased. The sample must be large enough to give every unit its proper weight. Here are a few statistical approaches to help you when you're stuck with inadequate data.

• Randomize. Although a very small sample can never adequately represent a large, complex population, randomization reduces the likelihood that your sample will be biased. After you've selected your sample, you can compare it to the population for known sources of variation. If there are large differences, you can increase your sample size, resample from scratch, or just keep the differences in mind when you perform your analysis and make your recommendations.

• Use sequential methods. If you're testing a statistical hypothesis, the usual approach is to take a sample n, calculate the test statistic, compare the statistic to a critical value or critical region, then reject or fail to reject the hypothesis. However, this isn't the approach to take if your goal is to minimize your sample size. A better way is to calculate the test statistic and make the comparison for every sample unit. In other words, look at the first unit, compare it to the critical value or region, then reject or fail to reject the hypothesis. If it's inconclusive, look at a second unit. Repeat until you've made a decision.

• Summarize data in large tables before analysis. When there are many categories of covariates, you may end up with tables containing hundreds or thousands of cells. If many of these cells contain no data, the table is said to be sparsely populated. One way to deal with this is to apply an approach called "smear and sweep." Smearing involves selecting a pair of classification variables and creating a two-way table from them. The values in the table are then swept into categories according to their ordering on the criterion variable.

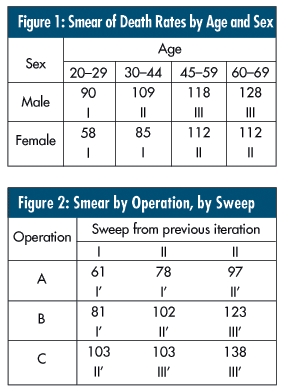Figure 1 shows an example of smearing death rates per 100,000 operations for a sample classified by age and sex, which are confounding variables. The sweeping is performed by creating a new category based on similar death rates, shown as Roman numerals. In this case, similar death rates across all ages and sex are reduced to three groups: I, II and III. These groups could be classified as "age/sex."

Figure 2 shows how the age/sex sweep variable is smeared with the new confounding variable "operation type" to create new sweep variables, I´, II´, III´. At this point the new sweep variable reflects the effects of the three confounding variables of age, sex and operation type. The process continues until all confounding variables are accounted for. If done properly (a lot of judgment is involved in selecting the cutoffs for the sweep variables) the smear- and-sweep method will produce less biased results than ignoring confounding variables. Some simulation studies show that bias may result from the application of smear and sweep, however.

About the author
Thomas Pyzdek, author of The Six Sigma Handbook (McGraw-Hill, 2003), provides consulting and training to clients worldwide. He holds more than 50 copyrights and has written hundreds of papers on process improvement. Visit him at www.pyzdek.com.