A
previous column addressed the assumption of data normalcy. You'll remember that one must assume normalcy in order to pursue capability analysis. Also recall that the chi-squared test is used to determine whether data is significantly different from normal.
Hartford Simsack has never understood chi-squared. Sometimes wondering whether it's a line of Greek pottery or a statistical formula, Simsack once again turns to his mentor,
Dr. Stan Deviation, for clarification of the method. Simsack wouldn't really care, except he knows that he'll have to demonstrate normal data before doing capability analysis. Deviation begins by
writing the chi-squared formula on his blackboard: 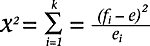
where fi = observed frequency for category i ei = expected frequency for category i k = the number of categories As Deviation begins to explain the formulas he's written, Simsack's mind goes blank and panic overcomes him. Nonetheless, he continues to nod and smile
knowingly, saying confidently that he understands this, of course, all the while wondering if there's another, less complicated method to check for normalcy. "I
need to avoid this chi stuff," he mumbles to himself. The professor says another method is to use probability paper. Hartford's ears
perk up. He loves gimmicks, and this certainly sounds like one. Maybe this new statistical tool will be something he can casually name-drop later with his
employees. Using a sheet of probability paper, Deviation shows Simsack how to fill it out. The steps are: 1. Form a frequency distribution.
2. Form a cumulative frequency. 3. Fill out probability paper. 4. Decide if the data create a straight line.
Thanking his mentor profusely, Simsack returns to the Greer, Grate and Gate plant and gathers 100 data points for an outer dimension that he's been
measuring. He goes through the data and derives the probability plot shown below: 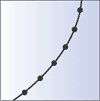
Squinting at the chart, Simsack tells himself that the line is straight enough to declare that his data reflect a normal distribution. What do you think? a) He's correct. b) He's incorrect. c) In this case, one can't be 100-percent sure if it's normal or not. Answer c is correct. As thousands of statistics students can attest, probability plots have been a
traditional favorite of college professors. Regardless of their relevance, they're easy to convert into test questions—something any instructor values. These
students, many of whom became consultants, introduced probability plots into training materials and even software.
The challenge of using probability paper, whether mechanical or computerized, is that after the line has been drawn, one has to consider whether the line is
straight enough to be considered straight. Rarely does a set of data points fall into an exact straight-line pattern. 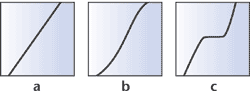
In the examples shown above, a is clearly straight, and c is clearly not. But
what about b? And what about the infinite number of b's that could be drawn? Whether the line is straight or not could be subject to debate, although there are
other statistical probability calculations that might help. On the other hand, a histogram—although still subject to judgment—gives a
much clearer view of the data itself without relying on one's ability to draw—or identify—a straight line.
About the author Michael J. Cleary, Ph.D. is a professor emeritus at Wright State University and founder of PQ Systems Inc. He has published articles on
quality management and statistical process control in a variety of academic and professional journals. E-mail Cleary at mcleary@qualitydigest.com .
Letters to the editor regarding this column can be e-mailed to letters@qualitydigest.com . |