How many times have you seen reports containing such statements as "The average diameter of bearings in the lot
is 0.5768 inches" or "The proportion defective of last month's production is 0.0024" or "The process Cpk is 1.15"? In most cases, these statements are based upon sample data from a much larger
population than the statements would indicate. Statistics, by their very nature, are really just estimates of the truth and, as such, are subject to error. The magnitude of
the error we encounter is a function of the sample size from which the statistic is calculated and the level of confidence we want to associate with the subject statistic.
When we report a Cpk of 1.15, the reader might assume that this is the true Cpk, when in fact 1.15 is just an estimate. A better way to report this result would be as follows: "I don't know
the true Cpk, but based upon a random sample of n = 45, I am 95-percent confident that it's between 0.89 and 1.41." Did you say between 0.89 and 1.41? That's like
telling a highway patrol officer you're 95-percent confident you were going between 35 and 190 miles per hour before you were pulled over. When you consider that a very bad Cpk is less than 1.00
and a great Cpk is greater than 1.33, the range of 0.89 to 1.41 is essentially meaningless. So what's the problem here? Either the sample size is too small or the confidence level needs to be
adjusted. The original Cpk of 1.15 is what we refer to as a "point estimate." By adding and subtracting the error, we get 0.89 and 1.41. This is an example of a 95-percent
confidence interval. The confidence interval for Cpk is calculated using the following formula: Cpk confidence interval = 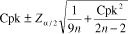
Equation 1
Where Cpk = the point estimate = 1.15 n = the sample size = 45 Note: The sample size is assumed to be less than 5 percent of the total
population. Otherwise, it would be appropriate to apply the finite population correction factor. 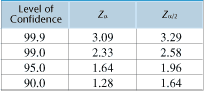 Za/2 = a constant for the level of confidence
= 1.96 for 95% (from Table 1) Za/2 = a constant for the level of confidence
= 1.96 for 95% (from Table 1)
For this example we have: 
1.15 ± 0.26, giving the 95% confidence interval of 0.89 to 1.41 What would the confidence interval be if we had determined the Cpk using a
sample size of n = 400 and the same confidence level of 95 percent? Using Equation 1, we have: Cpk = 1.15
n = 400
Z
a/2 = 1.96 
1.15 ± 0.09, giving the 95% confidence interval of 1.06 to 1.24 To express this in statement form, you could say, "I don't know the true Cpk,
but based upon a random sample of n = 400, I am 95-percent confident that it's between 1.06 and 1.24." This is a considerable improvement over the
confidence interval using a sample size of n = 45. What's the moral of this story? Don't use a small sample size.
In most practical applications of Cpk, we don't really care how large the Cpk is, but rather that it's not less than a certain value. What we actually want is the
lower confidence limit (LCL). This simply requires that we calculate a single-sided error by using Za rather than the Z
a/2 used in Equation 1. For the LCL, Equation 2 is used. Cpk LCL = 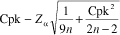
Equation 2 Example of an LCL for Cpk:
Assume a Cpk of 1.41 has been calculated from 150 observations. What is the lower 90-percent confidence limit for this estimate? Cpk = 1.41
n = 150
Z
a = 1.28 (from Table 1 at 90% confidence)
Cpk lower 90% confidence limit = 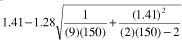
Cpk lower 90% confidence limit =
1.41 – 0.11
Cpk lower 90% confidence limit = 1.30 To express this in a statement, you could say, "I don't know the true Cpk, but based upon a random sample of 150 observations, I am 90-percent confident
that it's not less than 1.30" or "The lower 90-percent confidence limit for the Cpk based upon 150 random samples is 1.30."
So why is all of this error stuff important? Consider that the industry de facto definition of a "bad" process is one that has a Cpk of less than 1.00, and the
definition of a world-class process is one that has a Cpk greater than 1.33. The amount of error with a marginal Cpk = 1.15 and a sample size of n = 30 with a
confidence level of 95 percent is ±0.32. This means that the error of the estimated Cpk is 194 percent of the spread between a "bad" and "world class"
process. Now consider that all this talk about Cpk "assumes" a normal distribution. If your distribution is non-normal, the data is probably skewed to
one of the tails of the normal distribution (skewness > 0), and this is the very region where the Cpk will be most affected. Factor in the error due to
measurement and you see why Cpk has some serious flaws as a measure of quality. Even so, it's an index number that requires little effort to comprehend… Just be careful.
References Bissel, A.F. "How Reliable is Your Capability Index?" Applied Statistics 39, 1990, 331–340
Kushler, R.H. and Hurley, P. "Confidence Bounds for Capability Indices." Journal of Quality Technology 24, 1992, 216–231
About the author Mark L. Crossley is president of Quality Management Associates Inc. (www.qualman.com )
and is a CQE, CRE, CQA. He is the author of The Desk Reference of Statistical Quality Methods (Quality Press, 2000) and is a regular instructor for American Society for Quality courses in
introductory quality engineering and advanced topics in SPC. E-mail him at mcrossley@qualitydigest.com . |