by William A. Levinson If you know the enemy and yourself,
your victory is certain.
If you know yourself but not the enemy,
your chances of winning and losing are equal.
If you know neither the enemy nor yourself,
you will succumb in every battle. --Sun Tzu (~500 b.c.), The Art of War Traditional SPC methods assume that process data follow a normal bell curve distribution. Many real-world processes, however, don’t obey this convenient assumption. The semiconductor industry is very familiar with non-normal, skewed distributions for impurities and particle counts (note 1). It also uses many batch processes that involve nested variation sources. For example, vacuum chambers and furnaces apply thin coatings of metals or insulators to batches of silicon wafers (note 2). We expect the wafers in each batch or lot to see the same process conditions, but these conditions will vary randomly from batch to batch. Statistician Donald Wheeler explains the danger of lumping data together and using its collective mean and standard deviation to set control limits (Quality Digest, April 1997). In Wheeler’s example, using this “wrong” method can lead to burying the signals contained in the data, and the process seems to be in control. However, when the average range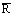 is the basis of the limits (the “right” way), it becomes obvious that the process is out of control. is the basis of the limits (the “right” way), it becomes obvious that the process is out of control. Or is it? This way assumes the rational subgroup is logically homogenous. But suppose the data are from a batch process with nested sources of variation. This type of data is very amenable to the methods used by Harris Semiconductor to handle nested sources of variation. Consider a heat treatment process for metal parts or for plastic or rubber productsfor example, polymer curing. A properly functioning oven or furnace will subject all the pieces in a batch to the same temperature for the same time. Unavoidable random temperature fluctuations within the furnace causes within-batch variation. Random differences between the conditions for each batch also will occur. Thus there are two variance components: within run and between run. The rational subgroup should be a random sample of the process’s overall performance. A sample of four pieces from a batch is not a sample of the overall process; it’s a sample of one batch and reflects only the within-batch variation, or batch uniformity. A batch or run, not a single part, counts as one independent measurement of the overall process (see Figure 1). If, however, the pieces go through a furnace on a conveyor belt, each piece is an independent measurement of the overall process (see Figure 2). N(u, sigma-squared) means “normal distribution with mean u and variance sigma-squared.” Under these conditions, traditional SPC should work properly. Statistical model for a batch process Here is the model for a batch process with only one level of nesting. The ith batch’s mean, u-subi is a random sample from the overall process. Pieces from the ith batch, x-subij, are then random observations from this batch.  Equation Set 1--Statistical model for a batch process: Equation Set 1--Statistical model for a batch process:
It’s easy to isolate the variance components when there’s only one level of nesting. Spreadsheet software can perform one-way analysis of variance (ANOVA) and deliver the necessary information.  Equation Set 2-- Isolation of variance components: Equation Set 2-- Isolation of variance components:
MSE and MST are the mean squares for errors and treatments, respectively. In his Design and Analysis of Experiments (2nd ed., pp. 7174), Douglas Montgomery discusses the procedure for nonconstant sample sizes. Let’s look at Wheeler’s data and assume that each subgroup is a batch: Table 1 shows the output from Microsoft Excel’s one-way ANOVA tool. (Corel Quattro Pro and Lotus have similar capabilities.) Pay close attention to the highlighted numbers. The F test shows significant between-batch variation; it rejects the null hypothesis that the batches have identical means. Next, use MSE (within groups) and MST (between groups) to find the variance components: and the correct limits for the averages chart are 5.00 ± 3 ¥ 2.706 = [-3.12, 13.12]. Although these limits look incorrect on an average chart, for a batch process with nested variation sources, they are correct. This is because the subgroups of four aren’t really what they appear to be. One batch is one independent representation of a batch process. We really have an individuals chart with six data points, not an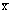 chart with six subgroups of four. chart with six subgroups of four. Range chart limitations The R (sample range) or s (sample standard deviation) chart should warn us if the process’s variation increases. A batch’s range, however, describes only the within-batch variation. Consider an oven or furnace that processes batches of parts. There will be unavoidable temperature variations between runs and unavoidable variation within batches. Suppose the factory treats four pieces from each batch as a subgroup of four. Something goes wrong with the temperature controller, and the variation increases. Because the temperature is uniform for each batch, the R or s chart will never detect the problem; it will merely warn the factory if the within-batch variation increases. This might happen in an oven, for example, if a convection fan stops working. On the other hand, a chart that treats four batch averages as a subgroup of four can detect an increase in between-batch variation. How do we know? Practitioners must always assess statistical models for conformance to the underlying assumptions. If the one-way ANOVA analysis is suitable for this data set, the model’s residuals (i.e., the observed minus expected values) should follow a normal distribution. Following are some tests from StatGraphics by Manugistics. (With only 24 data, the chi square test for goodness of fit cannot be performed.) The residuals should form a straight line on a normal probability plot (see Figure 3). Figure 4 represents the StatGraphics analysis. Note that none of the tests come close to rejecting the normality assumption for the residuals. 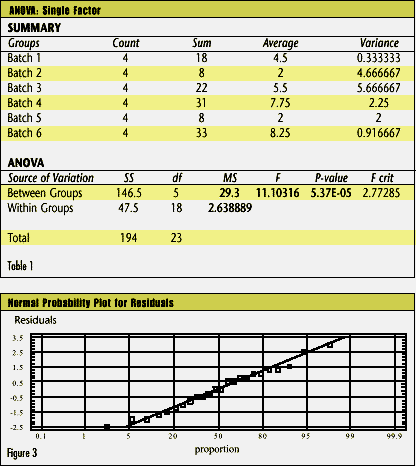 |
Many industrial processes do not obey the basic assumptions behind traditional statistical process controls. Practitioners should account for the process’s nature before developing control charts. One-sided specification limits (e.g., for impurities) are a clue that the data may be non-normal. Batch operations usually have nested variation sources. Techniques exist for assessing such nonideal data and setting control limits. Selection of the right model, however, depends on a proper understanding of the manufacturing process. References William Levinson, “Statistical Process Control in Microelectronics Manufacturing,” Semiconductor International, November 1994, pp. 95102. William Levinson, “Watch Out for Non-normal Distributions of Impurities,” Chemical Engineering Progress, May 1997, pp. 7076. Douglas Montgomery, Design and Analysis of Experiments, 2nd ed. (New York: John Wiley & Sons, 1984). Donald Wheeler, “Good Limits from Bad Data,” Quality Digest, April 1997, p. 53. About the author William A. Levinson, P.E., is a staff engineer at Harris Semiconductor’s Mountaintop, Pennsylvania, plant. He holds ASQ certifications in quality and reliability engineering, quality auditing and quality management. He is co-author with Frank Tumbelty of SPC Essentials and Productivity Improvement: A Manufacturing Approach and editor of Leading the Way to Competitive Excellence: The Harris Mountaintop Case Study (both copyright 1997, ASQ Quality Press). He can be reached at fax (717) 474-3279 or e-mail wlevinson@qualitydigest.com. 1. A one-sided specification is a clue that the distribution may be non-normal. This is especially true if the measurement cannot be less than zero (particles, impurity levels). Levinson (1997) shows how to fit such data to a three-parameter gamma distribution. The gamma distribution is the continuous scale analogue of the Poisson, which is a model for random arrivals. It is logical to treat particles and impurities as undesirable random arrivals. 2. Levinson (1994) includes a picture of wafers that are ready for metallization. The article also discusses multivariate systems, or processes with systematic within-batch variation. |

