Global warming is a theory in search of supporting data. However, in the search for supporting data, we should avoid misinterpreting our data.
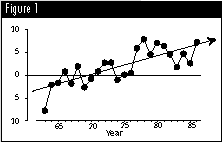
In the July 4, 1996, issue of Nature, Santer et al. use data such as those in Figure 1 as evidence of global warming. The values shown represent the annual average air temperatures between 5,000 feet and 30,000 feet at the midlatitude of the Southern Hemisphere. The zero line on the graph represents the normal temperature, and the values plotted are the deviation from the norm for each year.
The data of Figure 1 show a clear upward trend between 1963 and 1986. However, when we fit a regression line to data, we are imposing our view upon the data.
If we know of some cause-and-effect mechanism that relates one variable to another, then regression lines are appropriate. But does the year cause the trend shown in Figure 1? While regression equations are useful in showing relationships, these relationships may be either causal or casual. At most, the relationship in Figure 1 is casual.
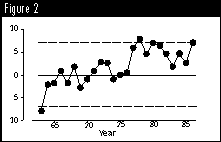
But is the trend in Figure 1 real? Or is it just noise? This question can be answered in two ways: Check for internal evidence of a trend with a control chart, and check for external evidence of a trend by adding more data as they become available. Figure 2 shows these 24 data on an X-chart. The values for 1963, 1978, 1980 and 1986 all appear to differ from the norm. Hence, the "cool" year of 1963 combined with the "warm" years of 1977 through 1986 do suggest a possible trend. So there is some internal evidence for a trend in these data.
The limits can be adjusted for this possible trend in the following manner. Compute the average for the first half of the data. Years 1963 through 1974 had an average of &endash;0.74° C. Plot this average vs. the midpoint of this period of time -- halfway between 1968 and 1969. Compute the average for the last half of the data. Years 1975 through 1986 had an average of 4.55° C. Plot this value vs. the point halfway between 1980 and 1981. Connect these two points to establish a trend line.
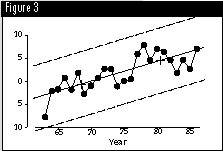
The distance from the central line to the limits in Figure 2 was found by multiplying the average moving range by the scaling factor of 2.660. The average moving range is 2.663° C. Thus, limits will be placed on either side of the trend line at a distance of: 2.660 x 2.663° C = 7.08° C (see Figure 3).
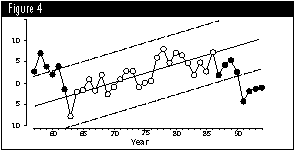
So the internal evidence is consistent with a trend for these data. But what about the external evidence? Professor Patrick Michaels of the University of Virginia added six prior years and eight following years to the data of Figure 1 (see Figure 4).
So, if the data for 1963 through 1986 are evidence of global warming, then the subsequent data show that we solved the problem of global warming in 1991. However, if the interpretation of the data for 1963 through 1986 is merely wishful thinking, then we may still have some work to do.
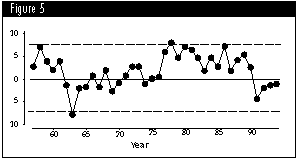
The 38 values are placed on an X-chart in Figure 5. Once again, the central line is taken to be zero in order to detect deviations from the norm.
So while 1963 was cooler than the norm, and while 1977 through 1990 were detectably warmer than the norm, there is no evidence in these data to support the extrapolation of the trend line shown in Figure 1. Obviously, there are cycles in the global climate, and any substantial evidence for global warming will require a much longer baseline.
The first principle for understanding data is: No data have meaning apart from their context. We cannot selectively use portions of the data to make our point and ignore other portions that contradict it.
The second principle is: While all data contain noise, some data may contain signals. Therefore, before you can detect a signal, you must first filter out the noise. While there are some signals in these data, there is no evidence of a sustained trend.
About the author
Donald J. Wheeler is an internationally known consulting statistician and the author of Understanding Variation: The Key to Managing Chaos and Understanding Statistical Process Control, Second Edition.