Content by Jody Muelaner

Thu, 03/05/2020 - 12:03
The seven basic tools of quality are a standard set of graphical methods for improving quality. They can help with understanding variation and determining the root cause of errors in processes. The seven basic tools are most commonly used within …
Wed, 01/29/2020 - 12:03
Understanding the causes of faults and defects, and then improving the system or process so it won’t happen again, is central to lean manufacturing. This article looks at some of the methods used to identify the root causes of issues so that you can…
Wed, 11/20/2019 - 12:03
Measurement is often seen as nonvalue-added work. However, if we properly account for the expected costs involved in passing defects on to customers, then the increased value of the product can be clearly shown. This approach makes it possible to…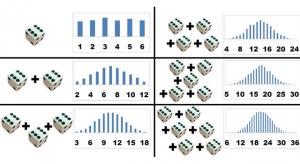
Thu, 10/31/2019 - 12:03
One of the key ideas in lean manufacturing is that defects should be detected as early as possible. Efforts to control manufacturing processes, so that issues can be detected before defects occur, actually predate lean. Statistical process control (…
Mon, 10/14/2019 - 12:02
How would you like to go hands-free, maintain visual focus, and save time? These are just some of the benefits of using voice command to control machinery. Increasingly sophisticated natural language processing, based on artificial intelligence,…
Tue, 10/01/2019 - 12:02
Attribute gauges are a type of measurement instrument or process that gives a binary pass/fail measurement result. Examples of attribute gauges include go/no-go plug gauges, feeler gauges, and many other types of special-purpose hard gauges. Many…
Mon, 09/30/2019 - 12:02
I’ve written a lot about how to evaluate the uncertainty measurements. My articles have ranged from basic introductions to metrology and uncertainty budgets, to more advanced topics such as sensitivity coefficients and Monte Carlo simulation. To…
Tue, 08/06/2019 - 12:03
In a general sense, capability is the ability to do something. Within manufacturing, capability is given a much more specific definition. It is an expression of the accuracy of a process or equipment, in proportion to the required accuracy.
This…
Tue, 06/11/2019 - 12:02
Whether we like it or not, manufacturing is becoming digitized and connected. Industry increasingly connects production machinery with internet of things (IoT) devices, gathers multiple real-time sensor information into large datasets, and harnesses…
Thu, 12/06/2018 - 12:02
In this article I will show that the conventional method for calculating uncertainty is not always reliable. In fact, it is generally only exact when the measurement can be represented by a simple linear equation and the input uncertainties are all…