Taking Count Data a Step Further
I recently received a phone call from a distraught hospital quality assurance director. A cardiologist had just left her office after screaming that "something needed to be done" about two of his colleagues who were "above average" in having their patients experience a very undesirable incident during a particular procedure, and he had the comparative bar graph of each physician's recent performance to prove it:
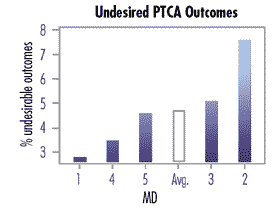
During this time period, 336 patients had undergone the procedure, and 16 had experienced the incident--an overall rate of 4.76 percent. One must now calculate for each individual physician's performance (i.e., stratify) the common-cause limits of what would be expected due to statistical variation, given the assumed 4.76-percent incident rate and the individual's number of procedures performed. Based on the appropriate statistical theory for percentage data based on counts (i.e., binomial), standard deviations must be calculated separately for each physician because each performed a different number of total procedures.
In this case, the standard deviation formula is:

Note its similarity to the "rate" calculation presented last month. The numerator of the square root is always the overall "system" percent multiplied by (100 minus the "system" percentage).
This result of the square root is then multiplied by three (for "three standard deviations," which will be explained next month) and added and subtracted to the overall mean to see whether the actual value for an individual physician is in the range of this expected variation, given an assumed rate of 4.76 percent.
Thus, for the given data,
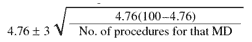
is now used to create the table below. The actual data are also shown, specifically, the numerators and denominators making up the individual percentages. Note that the only difference in each calculation is the denominator in the square root.


None of the physicians is even close to the upper limit. There are no outliers, either above or below average. Note that if a physician had zero occurrences of the incident, that still wouldn't be considered below average (i.e., exceptional performance), given the number of procedures performed at this point.
Based on this data so far, we can draw two conclusions. First, this practice is "perfectly designed" to have 4.76-percent undesirable incidents and, second, there's no difference in physician performance. The two previously designated "above average" performers are no different from their colleagues. The process producing these two physicians' results seems to be the same as the process producing their colleagues' results.
Davis Balestracci is a member of the American Society for Quality and the Association for Quality and Participation. He previously served as chair of the statistics division of ASQ. His book, Quality Improvement: Practical Applications for Medical Group Practice (Center for Research in Ambulatory Health Care Administration, 1994), is in its second edition. Visit his Web site at www.dbharmony.com.
|