An Alternative to the Red Bead Experiment
Management by flipping coins (MBFC)
W. Edwards Deming himself called it the "stupid" red bead experiment. I've used the following alternative for more than 15 years. It's a lot briefer (~10-15 minutes), makes the same points and people who've done both agree that it's more intuitive for audiences.
Step 1 . Count the number of people in the room ("N"), calculate (0.25 x N) + (0.433 x square root N), round it up to the closest number ending in 0 or 5 (like all good goals) and set this number as their goal ("G"). Any number greater than or equal to G is "green" performance. (If your calculation ends in 0 or 5, then make G this number; "green" then becomes any number greater than G.) Establish "yellow" and "red" regions with similar boundaries of 0 or 5.
Step 2 . Ask each participant to flip a coin. For those who get heads, have them flip again.
Count the number of participants who got double heads and compare it to the goal.
Step 3 . If they obtain the goal (which will be less than 15 percent of the time), praise them, but if they don't, throw a tantrum using phrases like "work harder," "work smarter," "stand up and be counted" and "march to the sound of the drums." (Then say, "Help me; I've run out of clichés.") As a final exhortation, threaten them with, "Let's have results instead of alibis… or heads will roll!"
Step 4. Repeat steps 2 and 3 for the second data point. React to the color, calculate the percent change from the previous flip or even some kind of variance from the goal, project the trend and make note of the "lazy" tables.
Step 5. If they've met the goal twice (very rare), then stretch them to the next 0 or 5 level and proceed with step 6.
Step 6. Declare that you're now going to use data to improve the process:
• Find those who obtained double heads twice.
• Promote these people to directors of coin flipping (DCF).
• Ask for a show of hands from those who haven't obtained a double head at all (about half). Follow-up with, "This is nonpunitive, and your names are…?"
• Optional: Divide these people into groups and assign them to a DCF for training.
Step 7. Repeat steps 2 and 3 to see the benefits of the training.
Step 8 . Compare their pattern of three numbers to the six possible patterns. (See my February 2005 column, "SPC in the Boardroom?")
Step 9. Generate an np chart with the data.
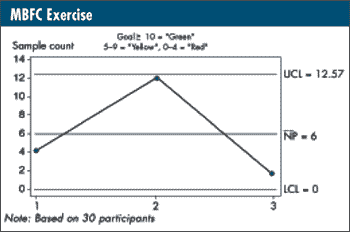
(I conducted a seminar this past week with 30 people, yielding a traffic-light system with ≥10 = green, 5-9 = yellow and <5 = red. We got an undesirable setback pattern of 4 red, 12 green and 2 red. The success rate was: (4 + 12 + 2)/(3 × 30) = 18/90 = 0.2, which resulted in the chart below.
Thus, in a roomful of 30 people, the expected range of double heads is 0-13 and contains red, yellow and green points, even though the 4, 12 and 2 are indistinguishable!)
At the end of the demonstration, ask whether someone got all three double heads. You'll probably get at least one person and be able to point out that individual performances in the room ranged from 0 to 100 percent!
Here are the major points:
• Every flip presented myriad ways to find "special causes" and actions to "fix" them. Because the chart shows the variation to be common cause, reacting to individual process results and individuals' performances is a no-yield strategy.
• Rather than asking, "Why are these numbers different?" try, "Is the process that produced the first result the same as the one that produced the second result, which is the same as the process that produced the third result?" The chart shows this to be true, so any comparisons are invalid (e.g., percent change, projected trend).
• You can then ask participants to flip the coin once and count the number of heads. Usually, this value will exceed your calculated upper control limit, and you can emphasize that a different process produced this result. (As in my example above, there's a very good chance that 30 people flipping a coin once will obtain greater than 13 heads.)
• Currently, the process is perfectly designed not to meet the goal. Making the goal "tough" and enforcing it through red, yellow and green interpretations distract from the true underlying performance and needed common-cause strategy.
• Given three flips, it's impossible to distinguish individual performances, even though they range from 0 to 100 percent.
Davis Balestracci is a member of the American Society for Quality and past chair of its statistics division. Visit his Web site at www.dbharmony.com.
|